Resistor networks involving parallel and series combinations of resistors can become quite complex as they get bigger and bigger. What about when they get infinitely big?
This post will assume you know the rules for calculating resistance of parallel and series combinations of resistors. It is a question similar to the kind of questions asked in the PAT, so this will be good practice for anyone sitting that soon.
Consider the following infinitely long resistor network, comprised of identical resistors each with a resistance of RΩ. Given the resistance converges, what is the total resistance in the circuit? Try it for yourself before looking at the working, and leave a comment if you find another way of doing this.
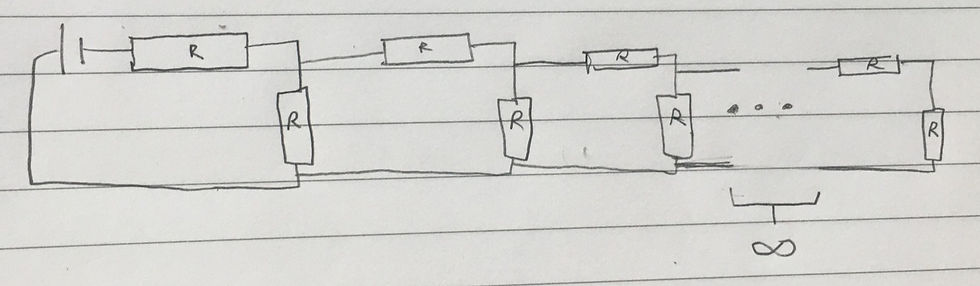
Where to even start? Well, the key here is to 'compress' the resistor network by representing combinations of multiple resistors as single resistors. Let's consider the resistance of the last parallel combination in the network. We can see that it is made of two resistors in series, in parallel with a single resistor. 'Compressing' the series resistor into an equivalent single resistor gives a resistor with resistance = R + R = 2R. Now we have a 2R resistor in parallel with an R resistor. If this combination were a single resistor (which we will call P1) it would have a resistance of the following:
Now the network looks like this:
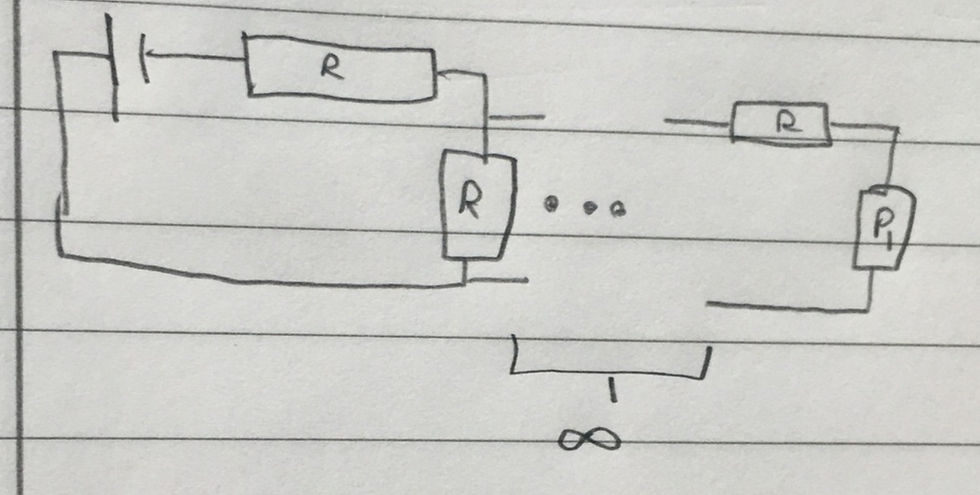
We can see that we have a single resistor of resistance P1 in series with one of resistance R. This is in parallel with a resistor of resistance R. 'Compressing' this combination into a single resistor gives a resistor we shall call P2 with a resistance of the following:
And a network that now looks like this:
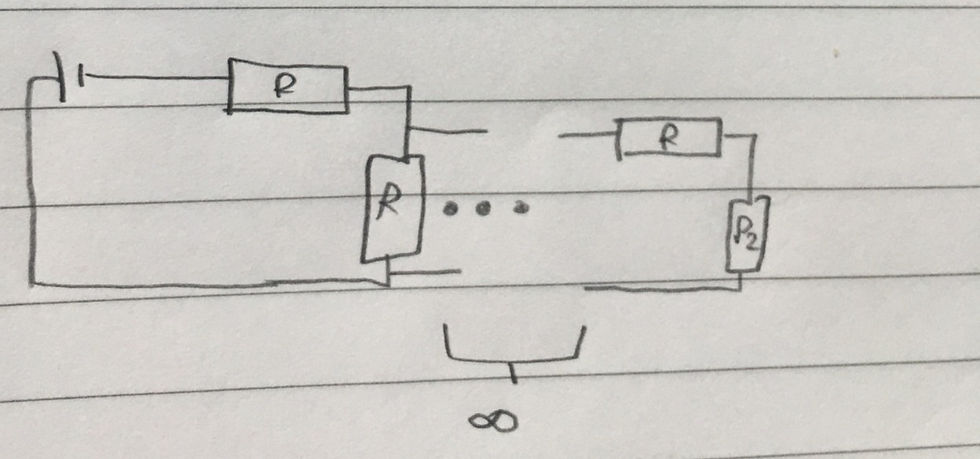
Let's do the same thing, combining the next parallel combination into a single resistor P3. From this we can clearly see a pattern:
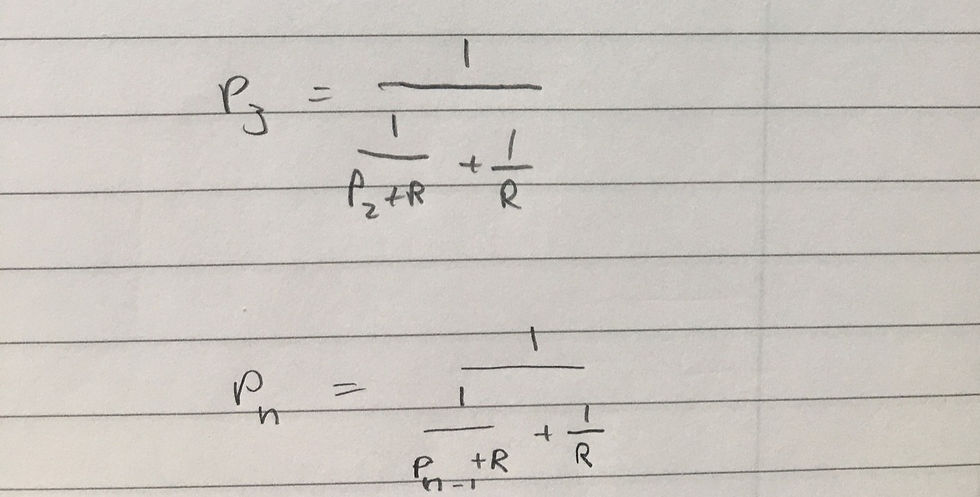
This gives us a sequence where each term in the sequence depends on the previous one. The question states that this converges. What does this mean? It means as the term number increases, difference between the next term and the current term gets smaller and smaller. In other words, as n approaches infinity, the resistance of the parallel combination approaches a limiting value.
How do we find this value? Well we know when the limit is reached, the current term will be equal to the previous term. If you have looked at an infinite number of terms, the current term will be equal to the limit, and therefore the next term you look at won't be any bigger. If this still doesn't make sense, don't worry; it will be covered at some point in the A Level Maths curriculum.
Anyway, as we know all terms after the limiting value has been reached will have the same value (the limiting value) we know Pn = P(n+1) = L. This lets us do the following algebraic manipulation to find L:
Here we simply rearrange the equation and solve the resulting quadratic in L. However, there are two solutions. There is only one limit, so one solution must be discarded. We know R>0 (can't have a negative resistance). This implies -R-√5R<0 and -R+√5R>0, so we need the positive root. From this we can get a value for the limit of the resistance of the infinite parallel combination. However, you may have noticed the original diagram has an additional resistor of value R in series with the infinite parallel combination. Using our resistor rules, we need to add this in to find the total resistance:
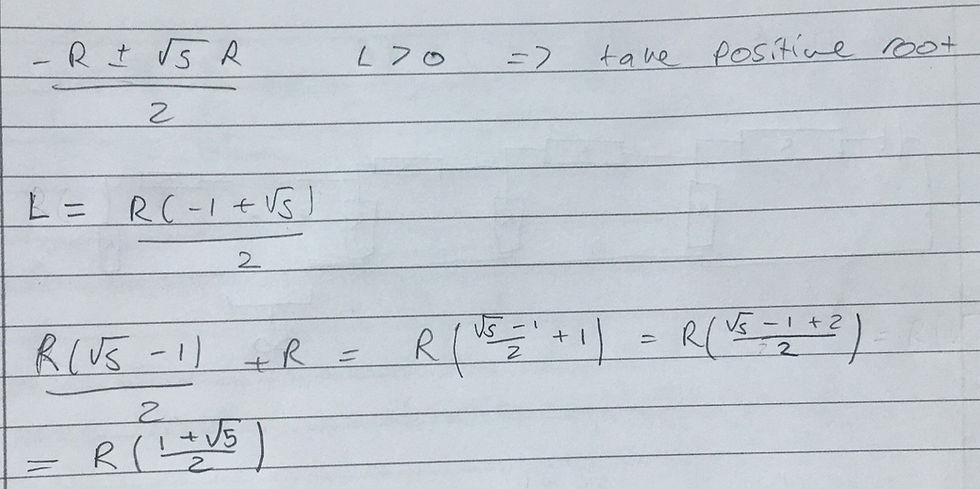
And we have our answer! Do you notice anything interesting about the final result? The term R is multiplied by is the known as the golden ratio, denoted φ. Therefore, a nicer version of the final result is simply φR. I'll leave it to you to work out why the golden ration appears here! Please leave a comment with questions or feedback and feel free to send me any questions you want help working through.
Comments