A-Level AQA Nuclear Physics Notes - #1
- Sep 4, 2020
- 7 min read
What are we going to learn?
In this post we will be focusing on the first two sections of the AQA nuclear physics specification (3.8.1.1 and 3.8.1.2). We will begin by understanding the Rutherford scattering experiment which you may have covered as a topic within your GCSEs but in slightly less detail than we will be looking at today. Then we will take a look into alpha, beta and gamma radiation as well as going through a required practical for the inverse-square law for gamma radiation. Finally, we will finish off the lesson with a real exam question testing the knowledge you have gained to make sure you understand the key concepts.

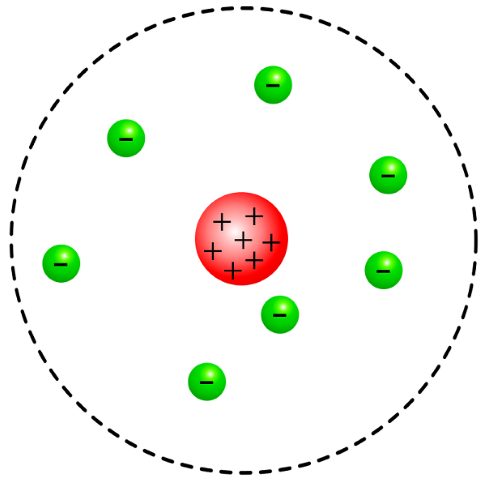
The Discovery of the Nucleus
In 1904 soon after the discovery of the electron, J. J. Thompson discovered that electrons could be removed from atoms and proposed that an atom was a ball of positive charge with electrons dotted within it. This was named as the plum pudding model. But later on in 1911, Ernest Rutherford conducted the Rutherford scattering experiment also known as the alpha particle scattering experiment. This led to the development of the nuclear model introducing the idea of a nucleus located in the centre of every atom. But what actually happened in this experiment which allowed Ernest to figure this out?

Rutherford Scattering Experiment
Rutherford knew that alpha particles consisted of positive charge and so did atoms. So he decided to take a sheet of thin gold foil and fire a beam of these alpha particles at the foil to see how they interact. Around the source and the foil, he placed a circular fluorescent detector screen which emitted a small pinpoint of light where an alpha particle hit it. This was due to the particles in the fluorescent screen exciting and then de-exciting to release photons which could only be detected with a microscope. During the experiment, Rutherford expected that the positively-charged alpha particles would be deflected by the electrons by a very small amount if the plum pudding model was true. Instead, most of the alpha particles travelled straight through the foil, and some were even deflected by a large angle sending them back the way they came.
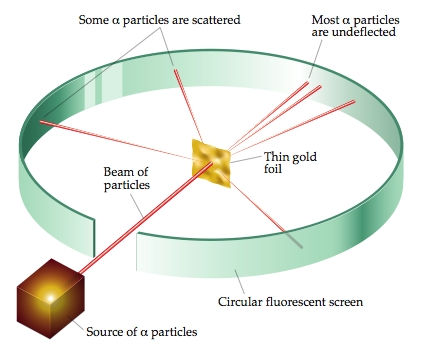
What did these results show about the structure of the atom?
Most of the atom must be empty space as majority of the alpha particles travelled straight through the foil
The positive charge must be concentrated at a single point within the atom (the nucleus) as some alpha particles were deflected straight back
The size of the nucleus must be small as few alpha particles were deflected back
Most of the mass must be in the nucleus, since the alpha particles with high momentum are deflected by the nucleus.
What variables had to be controlled during the experiment?
The alpha particles had the same speed because alpha particles travelling on the same path with different speeds would have caused different angles of deflection
The experiment had to be done within a vacuum chamber because air molecules would have caused interference with the alpha particles leading to an unreliable experiment.
The source of the alpha particles had to have a long half life so that later readings would not be lower than earlier readings due to radioactive decay.
After testing the gold foil, Rutherford began to test out various other metal foils. Using Coulomb's law of force and Newton's laws of motion, he was able to show that the magnitude of the charge of a nucleus is +Ze, where e is the charge of an electron and Z is the atomic number of the element.
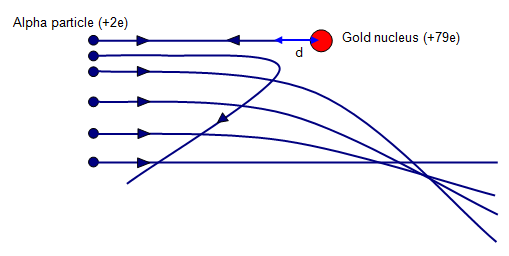
Estimating the closest approach of a particle
In the exam you may be asked to calculate the closest distance one particle can travel to another (for example, how close an alpha particle can travel to the nucleus).
This is a simple calculation which requires conservation of energy. You can simply calculate the kinetic energy of the moving particle and equate that to the electric potential energy between the two particles.
The equation for electric potential energy can be found by using Coulomb's law (as stated below) and using 'work done = force x distance'. You can simply multiply the equation below by 'r' (the distance between the two particles) to get the equation for electric potential energy.
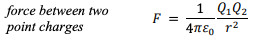
At this stage the process should be simple, you can calculate the kinetic energy with 1/2mv^2 and equate this to the electric potential energy.
Lastly, you would need to rearrange and solve for 'r' (the distance between the charged particles)
Alpha, Beta and Gamma Radiation
If a nucleus is unstable, it will break down to become more stable. This is often done by emitting particles or releasing energy. These particles tend to be alpha, beta or gamma particles. Here are the main properties you need to know:
Alpha particle (α)
A helium nucleus - 2 protons and 2 neutrons
Relative Charge: +2
Mass: 4u where u is the atomic mass unit (this is shown in your formula booklet)
Strongly ionising
Slow speed
Can be absorbed by paper or a few centimetres of air
Beta (minus) particle (β−)
Electron
Relative Charge: -1
Mass: negligible
Weakly ionising
Fast speed
Absorbed by approximately 3mm of aluminium
Beta (plus) particle (β+)
Positron
Relative Charge: +1
Mass: negligible
Annihilated by an electron so virtually zero range
Gamma (γ)
Short-wavelength, high-frequency electromagnetic wave
Relative Charge: 0
Mass: 0
Very weakly ionising
Faster than the speed of light
Absorbed by many centimetres of lead, or several metres of concrete
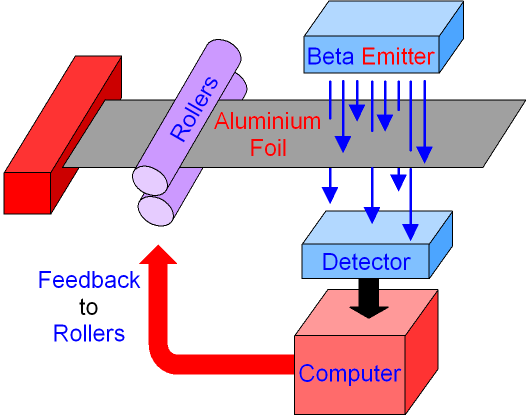
When a material is being flattened through rollers you can use a radioactive source and a radioactive detector to control the thickness of the material. A radioactive source is placed on one side of the material whilst a radioactive detector is placed on the other side. If a material is too thick it will absorb more radiation which means less radiation is detected and so the distance between the rollers can be decreased to produce thinner material. The same sort of concept applies if the sheet is too thin.
Hazards of ionising radiation
Ionising radiation is hazardous because it can damage all living cells.
It can destroy the cell membranes which causes cells to die.
It can damage vital molecules such as DNA which in turn affects cell division. Damaged DNA could cause cells to divide and grow uncontrollably, causing a tumour which may be cancerous.
Damaged DNA may also cause a mutation which is then passed on to future generations.
However, a high dose of ionising radiation is needed to kill living cells and cause cell mutation.
Background radiation is a measure of the level of ionising radiation present in the environment at a particular location and does not take into account the deliberate introduction of radiation sources. This is something which occurs naturally due to cosmic radiation and from radioactive materials in rocks, soil and the air. Here are the main sources of background radiation:
Air - radioactive radon gas is released from rocks and this is usually the largest contributor of background radiation
Medical
Ground and buildings - all rock contains radioactive isotopes
Food and drink
Cosmic rays - high energy cosmic rays collide in space to produce nuclear radiation
Living things - all plants and animals contain carbon, some of this is radioactive carbon-14
Nuclear weapons
Air travel
Nuclear power
Safe use of radioactive materials
Because ionising radiation is produced by radioactive materials, they must be stored and handled with care. This means the disposal of a radioactive substance must be carried out in accordance with specific regulations.
Storage of radioactive materials must be in a lockable lead lined container to reduce the gamma radiation and stop alpha and beta radiation from coming through.
Radioactive sources must be handled with tools such as tongs in order to increase the user's distance from the source allowing them to be beyond the range of alpha or beta radiation.
Liquid or gas sources and solids in a powdered form should be in sealed containers. This ensures the radioactive gas is not breathed in or the liquid is not splashed on anyone's skin.
The radioactive source should be used for as little time as possible to reduce the exposure to ionising radiation.
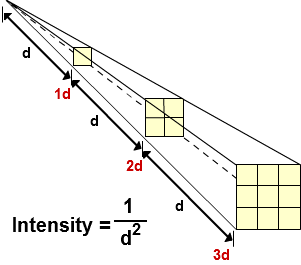
Inverse-square Law for Gamma Radiation
A gamma radiation source will emit gamma radiation in all directions. As you get further and further away from the source the radiation spreads out. This therefore means that the intensity (radiation per unit area) decreases as you get further from the source. If you measure the intensity at various distances from a source you will be able to observe that the intensity is inversely proportional to the distance squared. This is why one of the regulations when handling radioactive sources is to be as far away from the source as possible, because increasing the distance even slightly can significantly reduce the intensity of radiation.
Required Practical - Inverse-square Law for Gamma Radiation
You will need a Geiger counter which measures count rate in counts per second, radioactive source and a meter ruler.
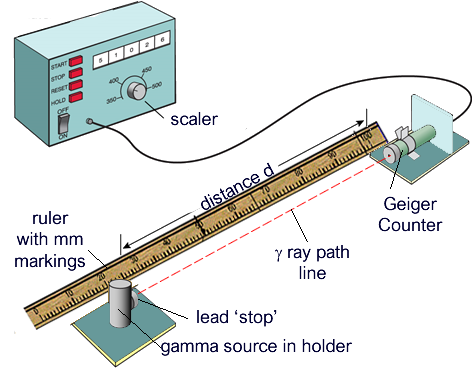
Turn on the Geiger counter and take a reading of the background radiation count rate. Make sure the radioactive source is left in the concrete container out of the way. Repeat this 3 times and find an average to get a more accurate reading of the background radiation.
Then place the radioactive source at 10 cm away from the Geiger counter, you can use your meter ruler to measure this distance.
Create a table of the distance between the Geiger counter and then 3 columns to take 3 readings of the count rate at each distance.
Record the count rate 3 times at each distance and calculate an average for each distance.
Increment the distance by 10 cm each time till you have recorded the count rates for at least 7 or 8 different distances.
Once you have taken all the necessary measurements, put your source away as you don't want to be exposed to more radiation than you need to be.
Correct each of your readings to account for background radiation by subtracting the background radiation from each average.
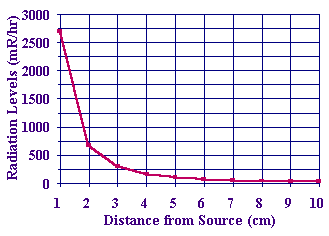
Lastly, you can plot a graph of the corrected count rate against the distance of the counter from the source. You should see that as the distance doubles, the corrected count rate drops to a quarter of its starting value which supports the inverse square law.
15 Minute Exam Question


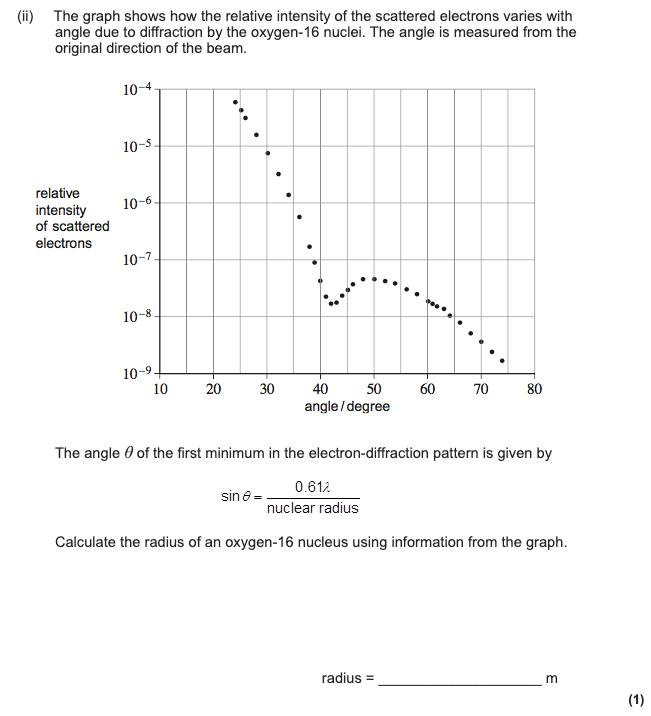

The Mark Scheme




Thank you for reading this post! If you have any questions please leave a comment and we will get back to you very soon. And remember to go read the next post of the AQA A-Level Nuclear Physics series, which focuses on Radioactive Decay and Nuclear Instability.



Comments