Area of a Circle Using de Moivre's Theorem
- Joel Runevic

- Nov 10, 2019
- 8 min read
Introduction
Some of you may be familiar with de Moivre's Theorem. This post isn't as so much me explaining something but rather just exploring a curious thought that I had. During a short in-class test on de Moivre's Theorem, after I had finished and checked my work, I became curious as to see whether one could use Argand diagrams to calculate the area of any shape formed by graphing the nth roots of a complex number.
Modulus-argument Form of Complex Numbers
Now, unfortunately, if you do not have a fundamental understanding of complex numbers, this blog will be a difficult read. But I will try and do my best to concisely explain as I go along. Essentially, a complex number can be represented in a Modulus-argument form, rather than the typical a + bi form that you may be comfortable with. On an Argand diagram, where the x-axis is replaced with the 'real axis' and the y-axis is replaced with the 'imaginary axis', we can neatly represent the Modulus-argument form of a complex number. This should derive the common expression r(cosθ + isinθ) for a complex number in Modulus-argument form, as I have shown in an image below:

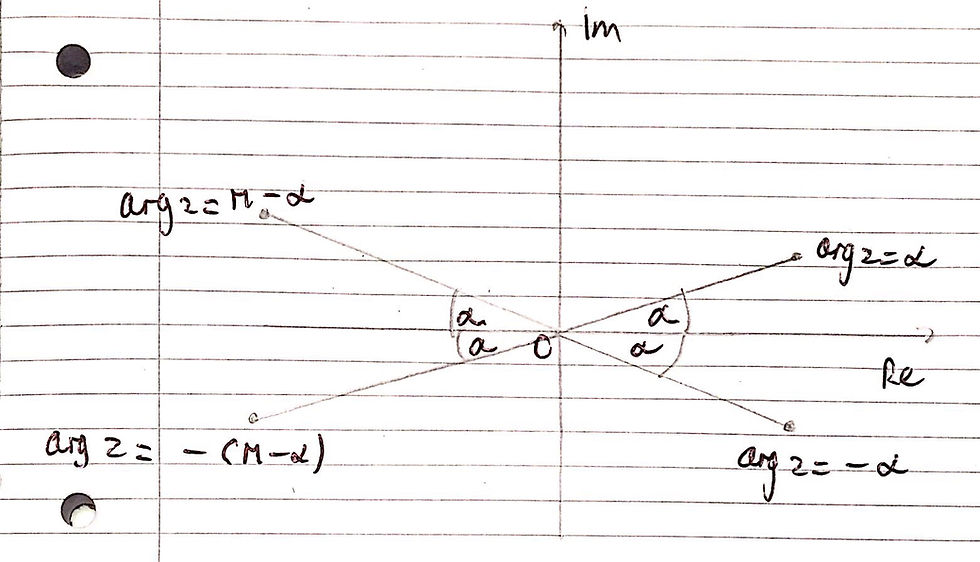
Keep in mind that the argument, θ, is usually given in the range -π < θ ≤ π and is measured anticlockwise from the positive real axis. I have included a diagram below showing the general rule:
de Moivre's Theorem
de Moivre's Theorem states that for any integer, n, the following is true:
( r(cos(θ) + isin(θ)) )^n = r^n(cos(nθ) + isin(nθ)). This can be proved using the method of proof by induction as I have done so below:


Roots of Unity
We can use de Moivre's Theorem to solve an equation of the form z^n = w, where z and w can be any complex number. If z = r(cosθ + isinθ) is a complex number, to find the
n-th roots, we can use the following expression:

The roots (otherwise known as the nth roots of unity) can be drawn on an Argand diagram. This will form the vertices of a regular n-gon. The angle between each root will be equal to 2π/n. For example, the roots of unity of z^5 = w (where, again, z and w are simply complex numbers) will form a regular pentagon, with an angle of 2π/5 between each root.
In order for you to see this method in action, I have included an example answer below (I used something called Euler’s relation at the end, which is just another way of expressing a complex number):


Exploring the area of the regular polygons
Now that you understand de Moivre's Theorem and how to find the nth roots of unity of a complex number, I can begin explaining a small problem that I came up with (to which I do not have a solution). When we sketch a said regular polygon with n sides, where n corresponds to the n-th root that we are trying to calculate, we can calculate the area of the regular polygon by splitting it up into smaller congruent triangles and by applying the sine rule for an area of a triangle (0.5*a*b*sinC, where C is the angle included by the two sides a and b). The values of a and b are identical and can each be represented by r, where, r, is the n-th root of the modulus of the original complex number.
Area of a circle?
We can therefore create a general expression for the area of any regular polygon, with n sides, formed by finding the n-th roots of any complex number, where r represents the n-th root of the modulus of the original complex number. I have included this general formula below:

It should be clear that I have just simply used the sine rule for the area of a triangle and replaced a and b with r^2. Moreover, sin(C) becomes sin(2π/n). Also, as there are n triangles formed, you must multiply the area of one triangle by n, in order to find the total area of the polygon formed. This formula holds for any n-sided regular polygon. I have included the square, from my previous example, as a further visual aid below:

However, my question to myself was; "What about a circle?". We can find the area of a circle using the known formula of πr^2. I have derived this using integration below (if you are interested at the derivation, have a look):



But how can we use our general formula, for the regular polygon formed by the n-th roots of unity, for a circle. Will n be equal to 0, 1 or infinity?. If we suppose, for simplicity, that the modulus of the complex number that is being n-th rooted is 1, then the value of r^2 will also be 1. This will simplify our general formula, in this case, to:
(n/2) * sin(2π/n). Our expected answer, using πr^2, should yield π. We can therefore compare the answer using our general formula/approximation to the known value of π (3.1415926535... ) to see how accurate our approximation is. This will, hopefully, allow us to find the value of n needed to calculate the area of a circle. At the time of writing this blog post, I do not know the solution; I am working this out as I go along!
Substituting n = 0, is not defined as you cannot divide a number, such as 2π, by 0. Substituting, n = 1, yields an answer of 0, which is clearly not π (this can be viewed as trying to work out the area of an infinitesimal point). The same result occurs for n = 2 as this is like trying to work out the area of a straight line. Therefore, if a circle, in this 'model', is not made up of 1-side then surely it must consist of an infinite number of sides? Can we then say n = ∞? Well, the issue is that, ∞, contrary to some people's belief, is not a number. Therefore, we can only analyse what happens as n approaches infinity, ∞. The value of n/2 approaches infinity as n approaches infinity, ∞, in other words, it diverges. The value of sin(2π/n) as n approaches infinity tends to 0, in other words, it converges. So what is the resultant effect? Is it ∞ multiplied by 0? Not quite, as neither value actually ever reaches infinity or zero. We are therefore multiplying an increasingly large number by an increasingly small number.
Substituting values provides clearly no help. Therefore, we can turn to geometrical analysis. Pictured below is a graph of f(x) = x / 2. As x increases, the value of f(x) increases by a constant amount (the gradient is constant).

Pictured below is also the graph of g(x) = sin(2π/x).

This is a very interesting graph. The function oscillates, however the frequency of the oscillations approaches infinity as the value of x gets closer and closer to 0. The function, like a 'normal' sine graph, oscillates between the values of -1 and 1. There is also an asymptote at x=0 as you cannot divide by 0.
Our general approximation is therefore the product of the two respective functions. In other words, h(x) = (x/2) * sin(2π/x). I have included an image of the graph below:

Focusing on values where x ≥ 0, like before, the frequency of the oscillations increases as x approaches zero. However, unlike before, the amplitude of each oscillation (the maximum y-value reached) is no longer constantly 1 but rather increases as x approaches 2. There is also an asymptote as x=0 as you cannot divide by 0. I say, 2, and not infinity, ∞, as after x=2, the graph seems to tend towards a value. Upon further inspection, the value of h(x) tends towards π; there is a horizontal asymptote at h(x) = π. I have Included the same graph but with the line h(x) = π also drawn to illustrate this, below:

Approximations
Thus, our general formula works for the finding the exact area of any n-sided regular polygon, however, for a circle, it is only an approximation. As we substitute a larger and larger value of n, our calculated area will get closer and closer to the ‘true’ value, π. It will never be exactly the same as we cannot substitute n=∞ but rather as n approaches infinity, our area will approach pi (π). You could also argue that it will never reach pi, as pi (the ratio of a circle's circumference to its diameter) is an irrational number and therefore its digits are non-terminating. Therefore, depending on the accuracy that you need, a sufficiently high value for n, will yield an accurate approximation for the area of the circle. Have a look below at the percentage errors involved in certain approximations for the area of the circle, using different values of n.
Value of π: 3.141592653 (to 9 d.p.). The percentage errors, even if r^2 is not equal to 1, will remain the same for each substituted value of n.
If n=10, the approximation is 2.938926261. This gives a percentage error of 6.5%. This is far too large for accurate calculations.
If n=20, the approximation is 3.090169944. This gives a percentage error of 1.6%. Although this is more accurate, it is still too large.
If n=30, the approximation yields a value of 3.118675362. This gives a percentage error of 0.73%. Still not accurate enough.
If n=50, the approximation yields a value of 3.133330839. The percentage error is now 0.26%, which is nearing acceptable values.
If n=100, the approximation gives a value of 3.139525976. The percentage error is mitigated to 0.07%, yet would still be considered a ‘good’ approximation at best.
Thus, n does not have to be immensely large for the approximation formula to give a relatively accurate approximation. At n=1000, we get 3.141571983 (0.0007% error), which will give an adequate approximation for the area of a circle, with negligible room for error. In fact, if I use n as, say 10^10, and put the formula into my calculator, my calculator displays π! I have included an image below:

The approximation doesn’t actually give an exact answer of pi but, since my calculator rounds all the answers to 9 decimal places, it must be equal to pi to at least 9 decimal places. This is a very accurate approximation indeed and our formula can be used to calculate the area of a circle drawn on an Argand diagram to a very high degree of accuracy.
Conclusion
You might be wondering what the point of all of this is, as you could simply use πr^2. Moreover, a circle will never be drawn on an Argand diagram as you can’t obtain the
∞-th root of a complex number. However, abstract questions, like the one we tackled today, allow us to gage a deeper insight into what we are learning. From one simple thought that came across my mind during a test, we have been able to understand how complex numbers can be represented on an Argand diagram, to proving de Moivre’s theorem by mathematical induction and subsequently used this theorem to find the n-th roots of a complex number. We didn’t stop there, as we are now able to draw the roots on an Argand diagram, as well as to be able to quickly calculate the area of the regular n-sided polygon formed using our own formula. We then graphed the said formula and were exposed to trigonometric graphs you normally wouldn’t see in school! Finally, we analysed the accuracy of the said formula as n approaches infinity. All this from one simple thought. I guess what I am trying to say is, as Eddie Woo, a well-known Australian maths teacher said; “Think deeply about simple things”. Thank you for reading this post!



Comments