Challenging Exam Questions: A-Level Maths #2
- Joel Runevic

- Jul 18, 2020
- 3 min read
If you are not a member of OnlyPhysics, please consider joining us - it's completely free and comes with loads of benefits, such as free online tutoring.
Welcome to the second challenging exam question on A-Level Maths. If you haven't checked out the first exam question, please have a look here: https://www.onlyphysics.
This question is going to test two important parts of A-Level Maths: arithmetic sequences and manipulating natural logarithms. The question is as follows:
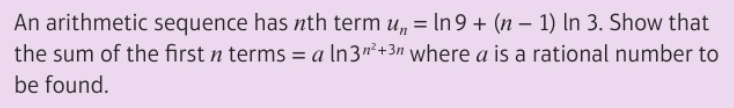
Okay, first things first, this may look pretty scary to you. It does seem like a very difficult question. We have n's in the powers and we have an unknown rational number, a, that we need to find. If you don't ground yourself and look at things that you do know, it can become a bit overwhelming very quickly.
So, what do we know. Well, we know that the first term in the sequence is ln(9). This can be worked out by just subbing in n=1 into the nth term formula that is given to us in the question. Now, in order to express the sum of the first n terms, we just need to know the difference, d, between each respective term. This is normally the coefficient of the (n-1) term, which in this case is ln(3).
Now that we know the first term of the sequence and the common difference we can create an expression for the sum of the first n terms for this arithmetic sequence. The equation for this can be found in your formula booklet - I have included an image for reference below:
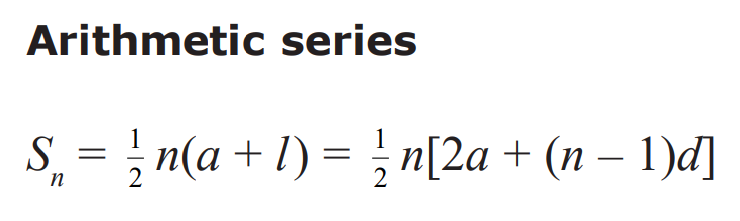
We know the value of a and d from our previous analysis. We also know that n just refers to the number of terms in the arithmetic series, so we can begin to work on the problem. We start off by just subbing in what information we have and know. I have included this in the image below:
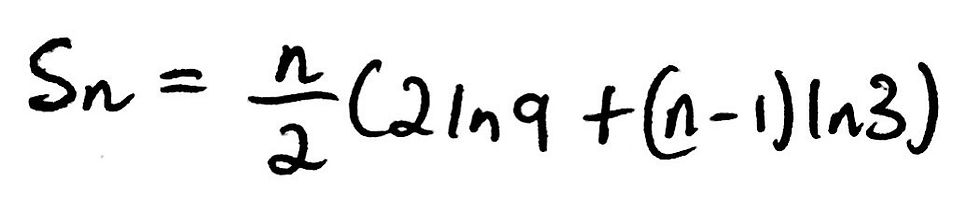
We can now begin to manipulate the expression to get something that looks similar to the given answer. Essentially, we need to simplify the natural logarithms into one equivalent natural logarithm. Looking at what we have, you should be able to see that 2ln(9) can be simplified to ln(81) as 9^2 is equal to 81. We can also expand the
(n-1)*ln(3) term to get two separate logarithms. I have included what we have done so far in an image below:
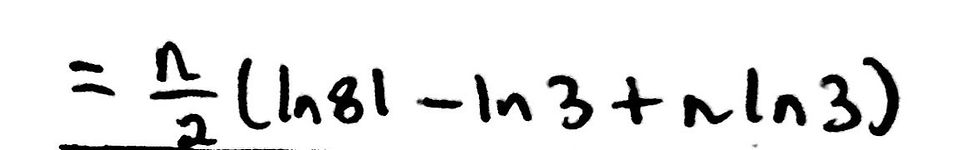
From the logarithm rules, you should be able to see that ln(81) - ln(3) can be simplified to ln(27). This quite a small but important step so I have included an image below for reference:
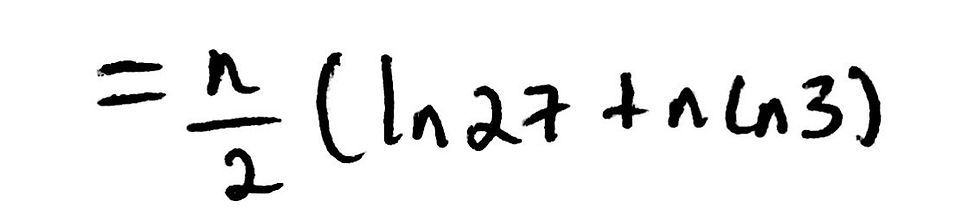
Now, this is where the magic happens. We have to get every logarithm to be in terms of ln(3). We can rewrite ln(27) as ln(3^3) and n*ln(3) as ln(3^n). This should be quite obvious from the rules regarding simplifying logarithms. Our current expression now looks like this:
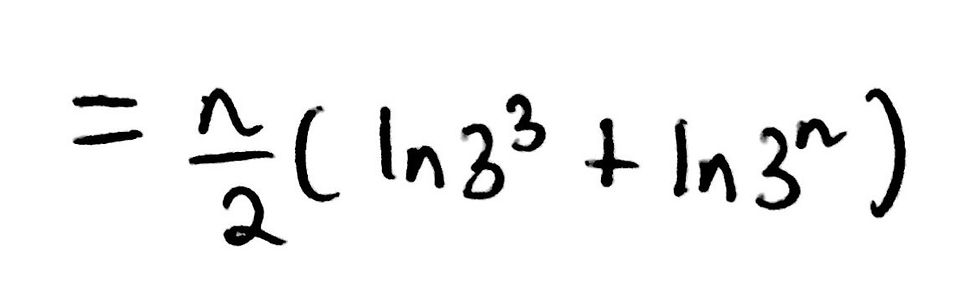
We can now simplify the final two logarithms. Remember, when you add two logarithms with the same base, you multiply the two numbers together. Here, we can simplify the two logarithms into one equivalent by using our indices laws. Multiplying 3^3 by 3^n is equal to 3^(n+3) as we can just simply add the powers together. Thus, we can simplify our expression to this:
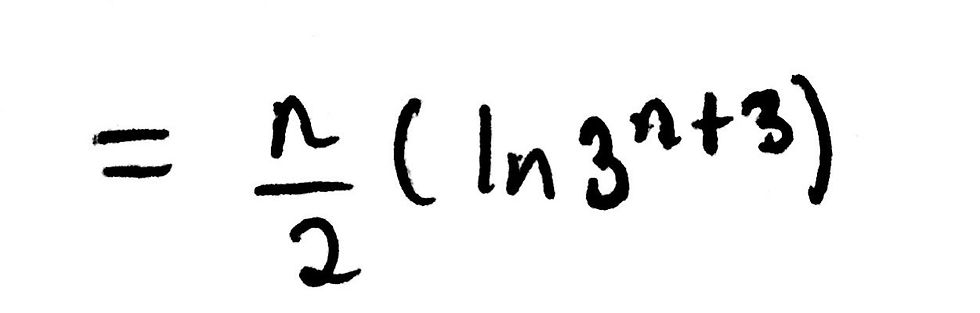
Looking at the answer that is given in the question, we are very close. I mean, it seems like each power is out by a factor of n. However, keep in mind that we have the coefficient n/2 in front of the natural logarithm. Therefore, we can, by using our logarithm rules, multiply the powers of the logarithm by n, effectively turning our n/2 coefficient into 1/2. This is the exact same process as when we turned the 2ln(9) into its equivalent ln(81), except this involves some algrebra. I have included an image of the final answer below:

So, there we have it! We reached an answer that is identical to the one given in the question whilst only using logical and sound mathematical reasoning. Don't forget, however, that we need to state the value of a. In this case, it is 1/2, as I have included in the image above. Be careful not to forget this last final statement as it may cost you that all-important answer mark!
Thank you very much for reading this post! I hope that it has been helpful to you. If you have any questions, post them down in the comments below. Stay tuned for Question #3!



Comments