Challenging Exam Questions: A-Level Maths #3
- Joel Runevic

- Aug 4, 2020
- 4 min read
If you are not a member of OnlyPhysics, please consider joining us - it's completely free and comes with loads of benefits, such as free online tutoring.
Welcome to the third challenging exam question on A-Level Maths. If you haven't checked out the second exam question, please have a look here: https://www.onlyphysics.org/post/challenging-exam-questions-a-level-maths-2
This question will stretch your understanding and knowledge of the product rule within the topic of differentiation - arguably one of the most important topics to grasp within the A-Level Maths spec.

Both questions seem very challenging and they are. Normally, when you see a question testing product rule either directly or indirectly, there are only two terms that you have to worry about. Here we have 3 algebraic terms in each question part. As you would in an exam, we are going to start by solving Part a.
Part a:
Now before we can begin to answer this question, you must be confident in knowing what the product rule actually is. Product rule allows us to differentiate the product of two functions: note that I said two. As soon as you see a product of two functions of the same variable - x in this case - you must apply the product rule.
There is a mathematical proof for the product rule; however, it is far beyond the scope of the specification. I can, however, include a derivation upon request, at the bottom of this post, for those who are intrigued by it. But, for those who just want to learn about the product rule to ace their exams, you just need to know the following:
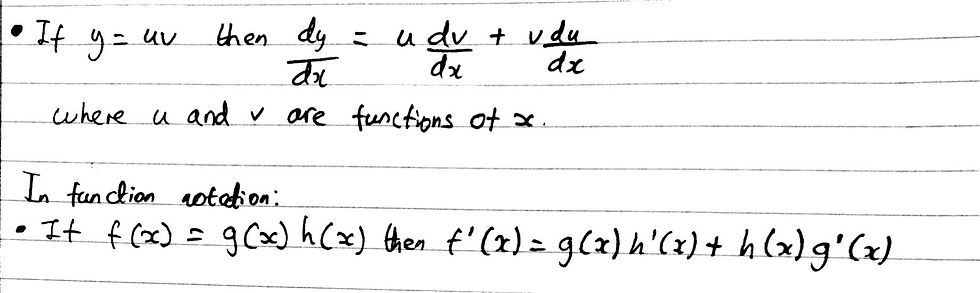
You may be a bit confused and be thinking; "how are we supposed to use product rule on 3 terms if it only works with 2?". The key 'trick' to this question is that we are going to use a product rule within a product rule.
We can split the three terms into two variables as shown below. Note that it is essential that you group the two trigonometric terms together as otherwise the question will become much harder to solve.
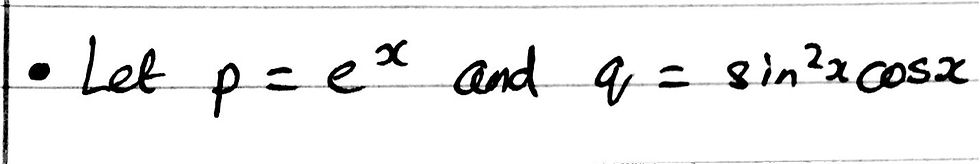
Now, we can represent the function as being equal to the product of these two variables. In other words, we can say that y = pq. This therefore makes it easier for us to differentiate the function.
From here, we can perform the product rule on y = pq. If we use the product rule formula, we know that the derivative of y with respect to x can be written as the following:
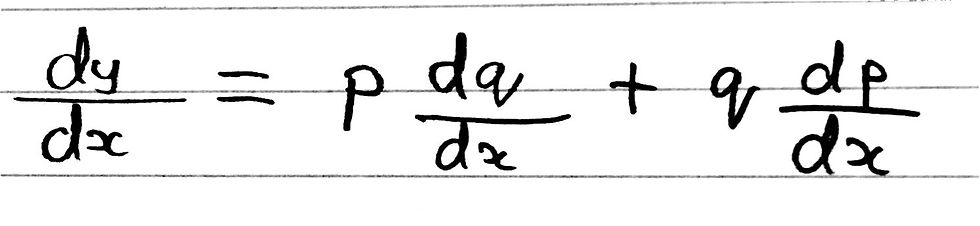
What is the point of doing this? Well, know we don't actually need to differentiate the product of three terms, but rather we simply can just differentiate two terms. You see we have now split up the problem into just working out what dq/dx and dp/dx are, as we have already assigned the values for the variables p and q respectively. Both of these derivatives only contain two or fewer terms and thus we can just apply the product rule again - this is what I meant by performing a product rule within a product rule.
We can work out dp/dx very easily by differentiating e^x, which is just e^x (this is a standard result that you should be familiar with). I have included an image below to make this clearer:
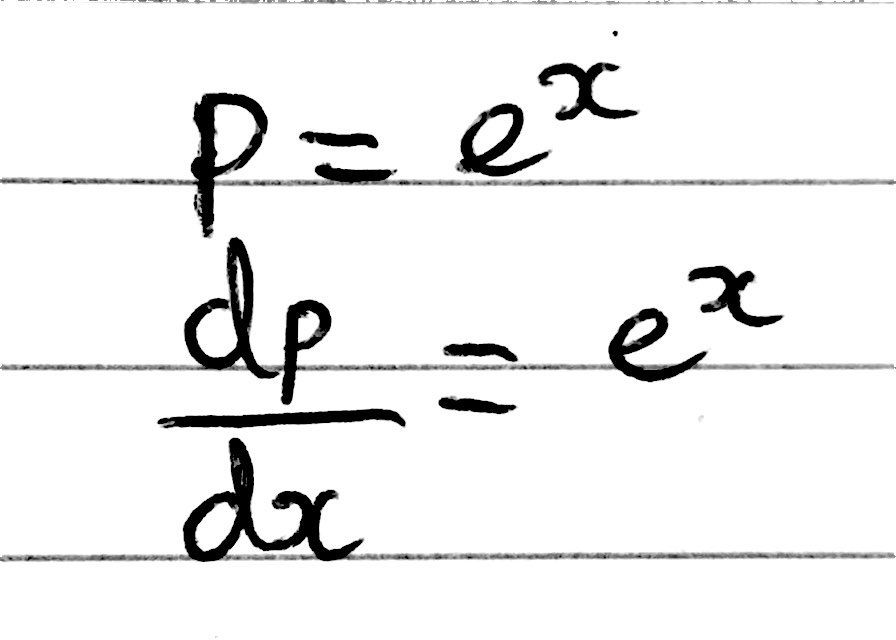
All we need to do now is work out the value of dq/dx. Essentially, we just have to differentiate the variable q with respect to x. We can do this by just performing the product rule on the variable q.
It should be clear that we can simply write out q as being equal to the product of two other variables, say, u and v. Thus, we can write q = uv. Subsequently, we can assign the variables u and v to sin^2(x) and cos(x) respectively. The reason why we assign the variables u and v is because it allows us to answer the question in a much neater and more concise manner. We can therefore now use the product rule to differentiate the variable q. Note that you must be familiar with the chain rule and differentiating trigonometric functions in order to finish the question off.
Firstly, we need to work out du/dx and dv/dx respectively. This should be quite easy if you are familiar with the chain rule. I have included an image of the relevant derivatives below:
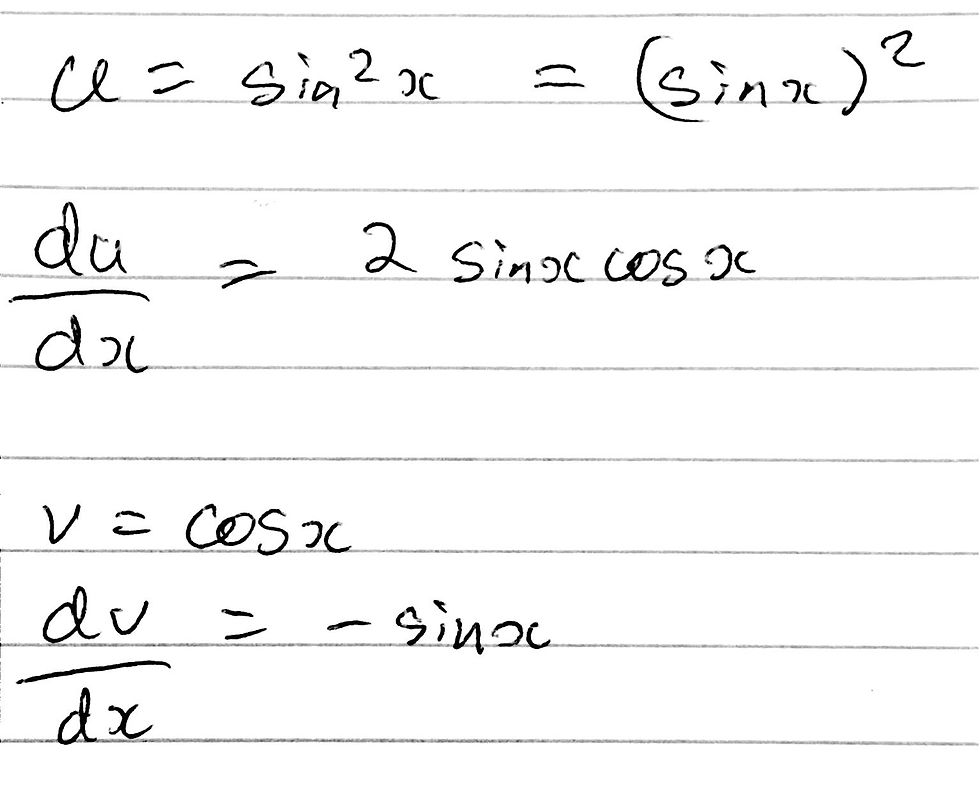
We now have the necessary differentials and we already know the values of u and v as we have assigned these earlier. Ergo, we have everything we need in order to calculate dq/dx using the product rule. We just have to substitute in the necessary values and simplify. I have included my workings in the image below:
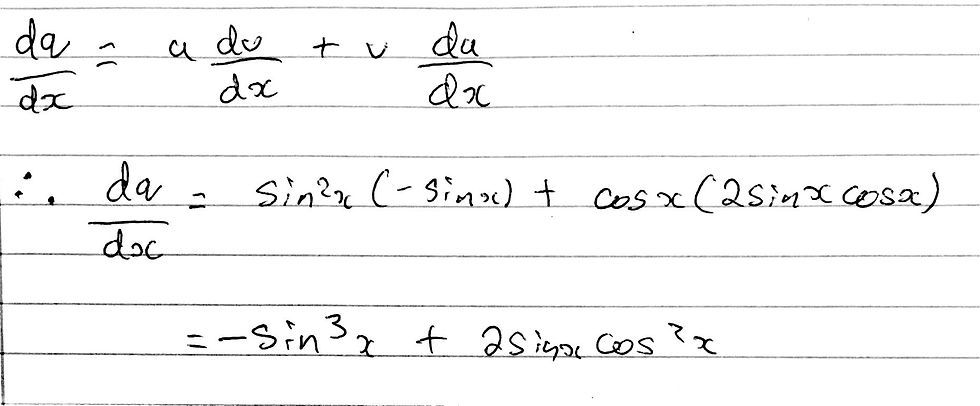
We are almost done with Part a! We have worked out expressions for both dp/dx and dq/dx and can now substitute these values in, along with the values for the variables p and q that we assigned earlier, to find a final expression for dy/dx, successfully differentiating our original equation with respect to x.
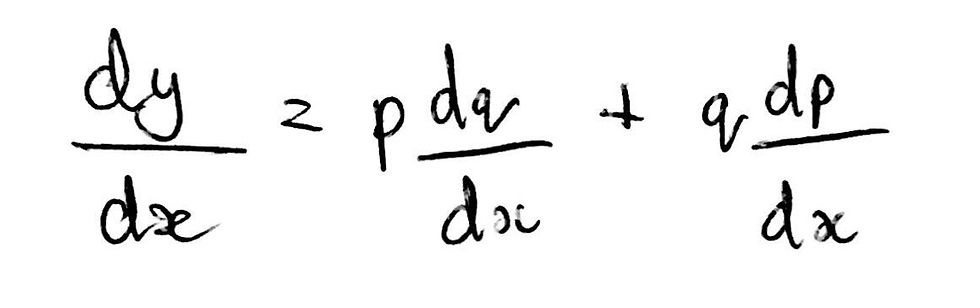
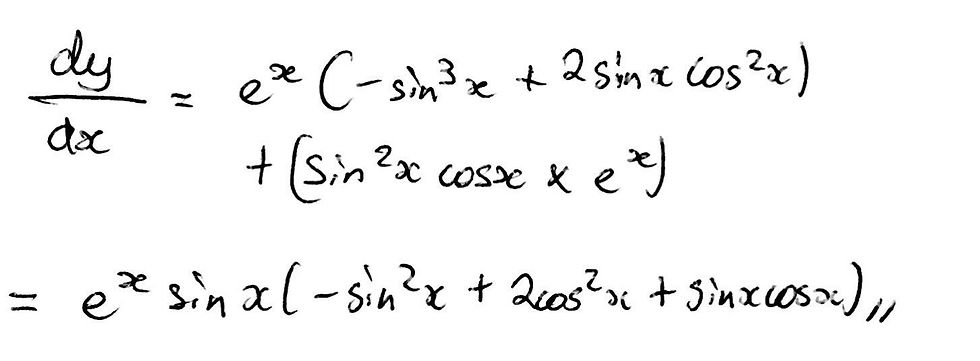
That is it for Part a of this question! As you can see, it is fairly involved but once you understand one little trick, it doesn’t become any more difficult than just performing simple differentiation using the product rule.
Part b:

Part b is very similar to Part a. In fact, we can just follow the exact same method. Have a go at completing this question before looking at the solution down below.
I am not going to explain the solution in detail like I did for Part a, as it follows the exact same reasoning as before.

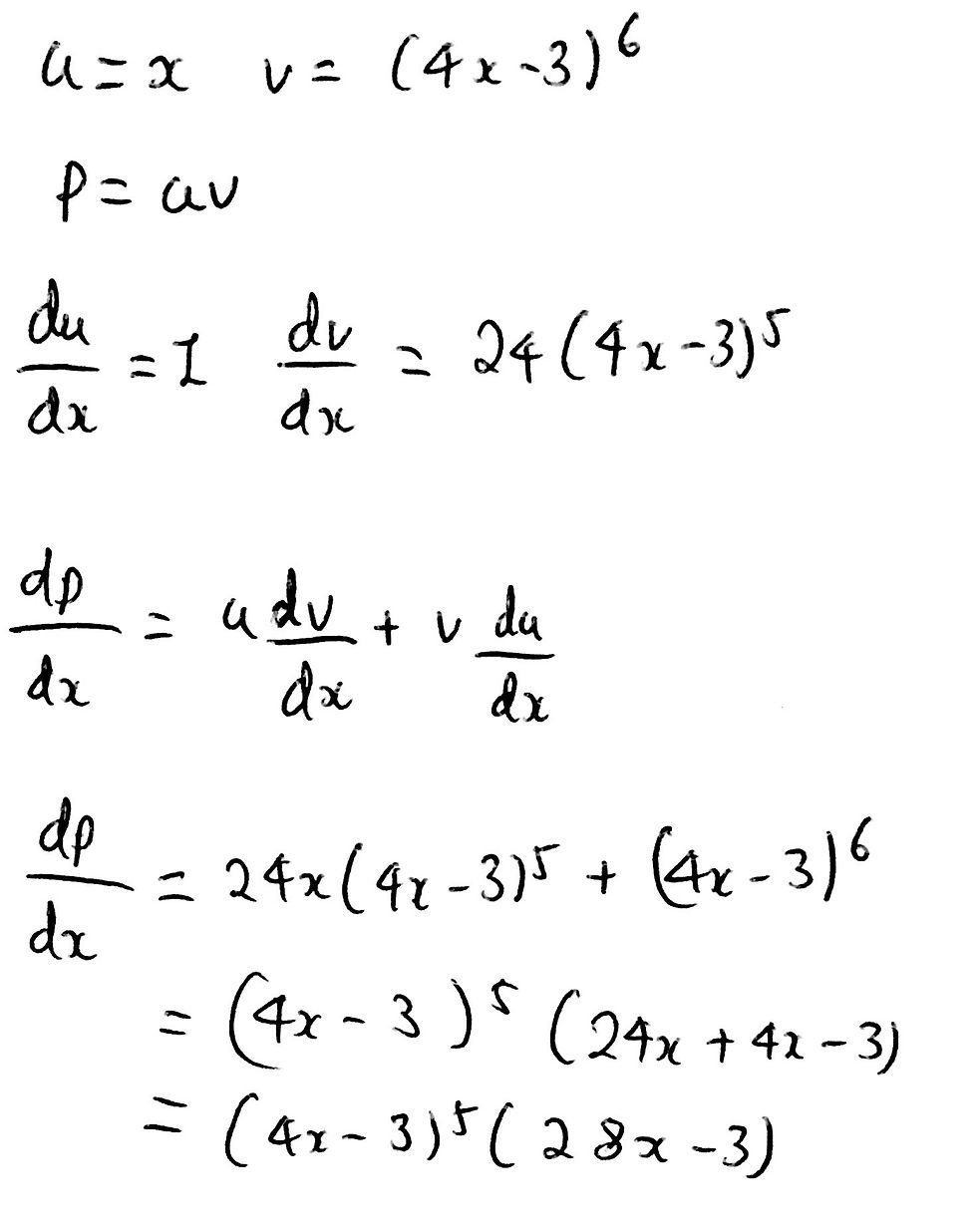

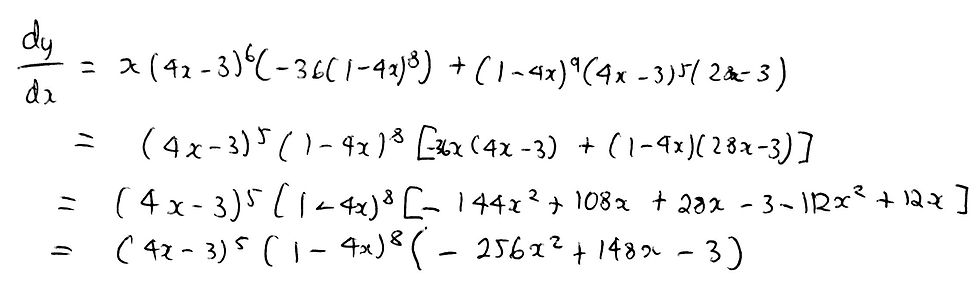
That is it for Part b of the question and for the entire question as a whole! Like I said before, part b followed the exact same logic as answering part a, so I didn't commentate on the exact process. I hope that you can now see how just by utilising one simple trick, you can simplify tough differentials into smaller ones that you have previously dealt with.
Thank you very much for reading this post! I hope that it has been helpful to you. If you have any questions, post them down in the comments below. Stay tuned for Question #4!



Comments