Hardest Questions on Oxford's Physics Aptitude Test 2019
- Joel Runevic

- Oct 9, 2020
- 13 min read
What is the PAT?
This post tackles the hardest questions on the PAT (Physics Aptitude Test). If you don’t know what the PAT is, it “is a subject-specific admissions test, lasting for 2 hours and sat under timed conditions”. It is essentially the Oxford Admissions Test for the following courses - Engineering, Materials Science, Physics, Physics and Philosophy. It is aimed at Year 12 Students in the UK - equivalent to Grade 11 in the USA and it is an extremely difficult admissions test. There is normally a cut-off mark for the test, resulting in the top 30% moving onto the interview stage.
Now, if you aren’t planning to sit the PAT, then this is still a very useful post for anyone who is studying Physics and Maths at High School. The test is arguably one of the most difficult University admissions tests out there and thus it is a great challenge for any budding physicists.
In this post, we will tackle the most recent admissions test cycle - PAT 2019. According to Oxford’s annual report on the PAT, for the 2019 admissions cycle, the mean mark was 41.45% (equivalent to approximately 41 raw marks on the paper) with a standard deviation of 16.76%. Thus, in order to have a good shot at admissions, one should be looking at a score greater than 50 marks.
The 2019 PAT was objectively harder than the 2018 PAT. Normally, the mean mark increases year on year; however, this year was an outlier. The mean mark for the PAT 2018 was 52.1%, about 10.7 percentage points higher than the mean mark of the 2019 PAT. But, not every question on the PAT is worth doing when you are revising as they can get quite repetitive. Moreover, the later questions, e.g. question 20, are not necessarily the most challenging to do. Thus, I have decided to create a post series on the biggest curveballs on each PAT, starting with 2019.
Question 14:

As you should be able to tell, this question tackles radioactive decay, which is a topic within nuclear physics. If you aren’t familiar with this topic, Hassan Bajwa has written a beautiful blog post on it, which can be found through this link: https://www.onlyphysics.org/post/a-level-aqa-nuclear-physics-notes-2.
This question is not the most difficult in the conventional sense; however, it does become very fiddly and challenging as you progress through the question parts. So, let’s begin.
Part a:
At one half life, half of the initial number of atoms would have decayed. Thus, we can substitute in the fact that there are Na0 / 2 atoms remaining after one half life has elapsed. From here, we can simply use algebraic manipulation as well as logarithms to find an expression for λ in terms of the half life. I have included the workings below. This would be considered an easy PAT question part, so let’s not get too excited just yet.
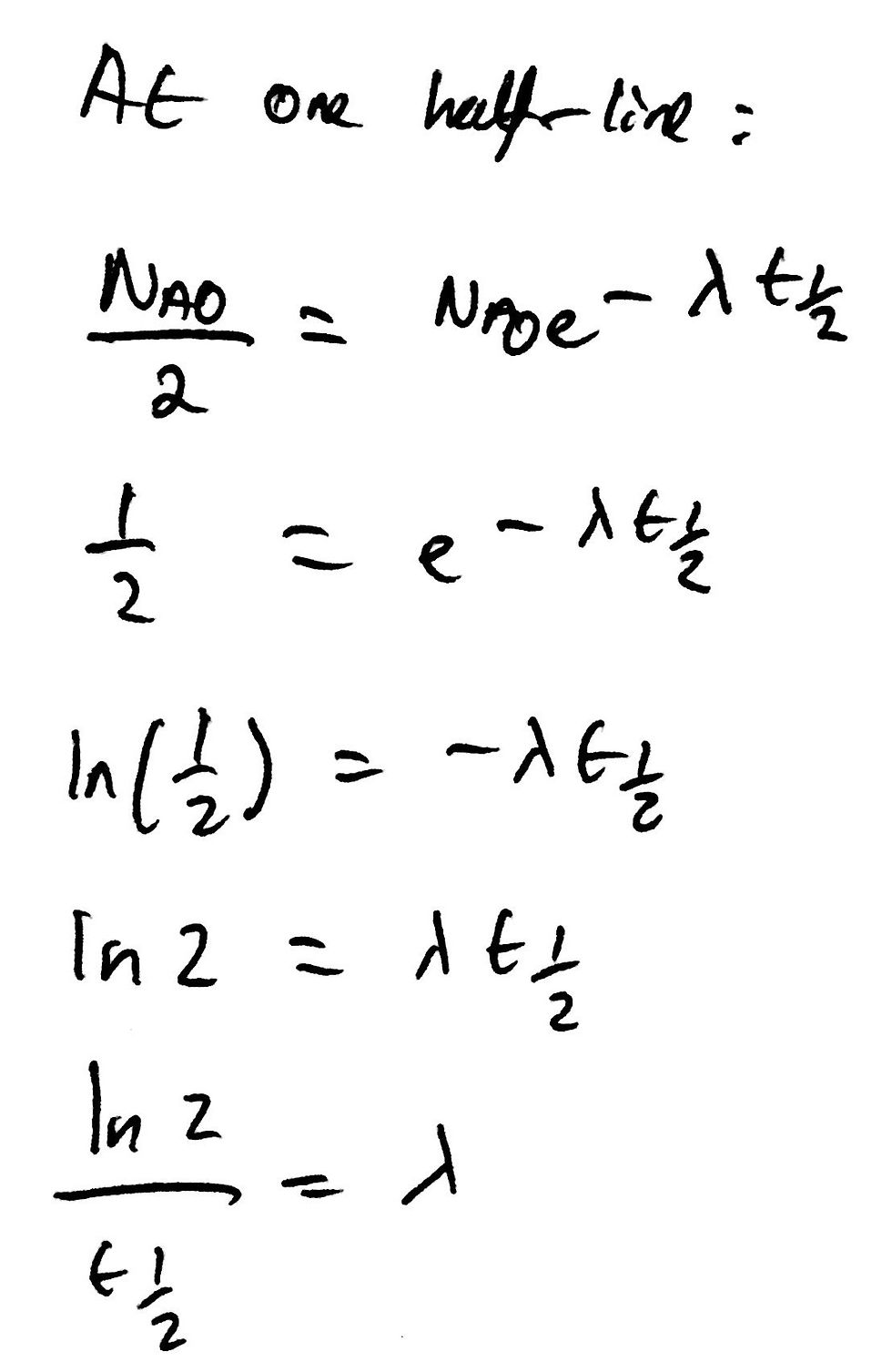
Part b:
The key to this part of the question is that isotope B is stable and will therefore not undergo nuclear decay. In order to determine how many B atoms are present at any point - Nb(t) in other words - we must consider two separate variables. Firstly, we know that the initial number of B atoms is Nb0, which is a constant. However, the current number of B atoms increases depending on how many A atoms have decayed. The value of Na(t) states the number of atoms of A left after a time t - we have been told this in the question. Thus, the number of A atoms that have decayed is simply the initial number minus the current number, or, in mathematical terms, Na0 - Na(t). We can therefore use our expression for Na(t) to simplify this more neatly. I have included an image of this below.
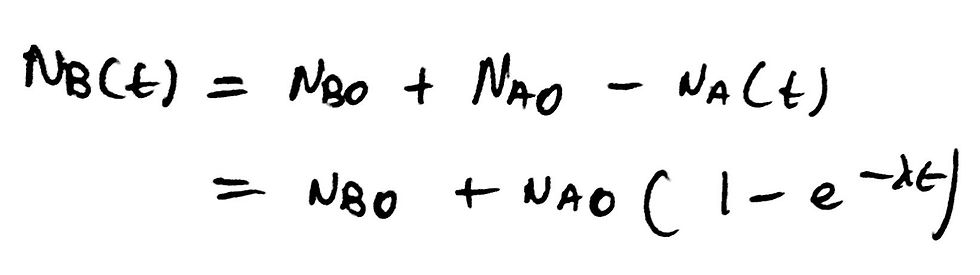
Part c:
This question part stated “at the start there are x times as many A atoms in the sample as there are B atoms.” Using this key piece of information, we can state that Na0 = xNb0. Note the use of Na0 and Nb0 respectively as this is the ratio relationship at the very start - before any radioactive decay has occurred. When this ratio is reversed, the following equation must be true: Nb(t) = xNa(t).
From here, we can substitute in our two respective expressions for Nb(t) and Na(t). We must also use the fact that xNb0 = Na0 as our second equation. This will allow us to simplify the original equation and arrive at a very neat expression for the time taken - t - for the ratio to be reversed.
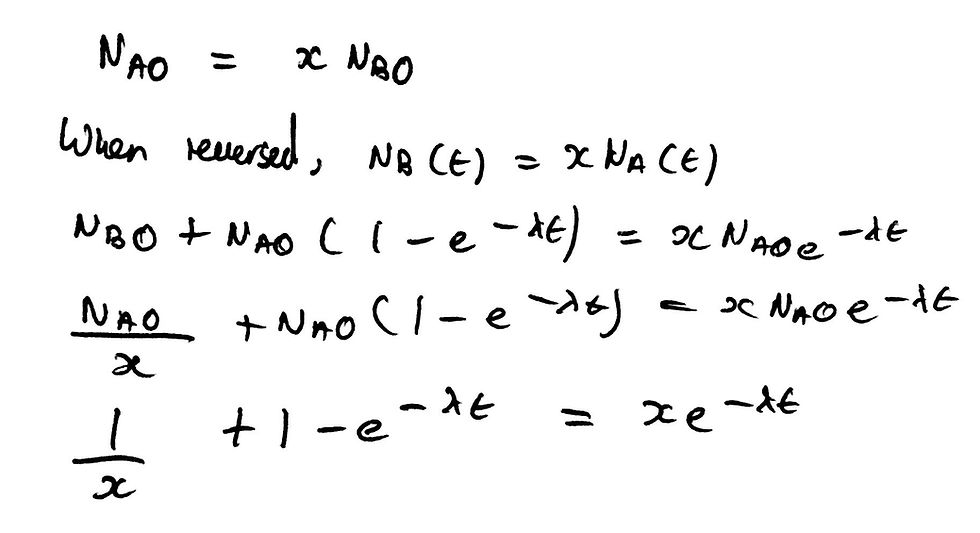
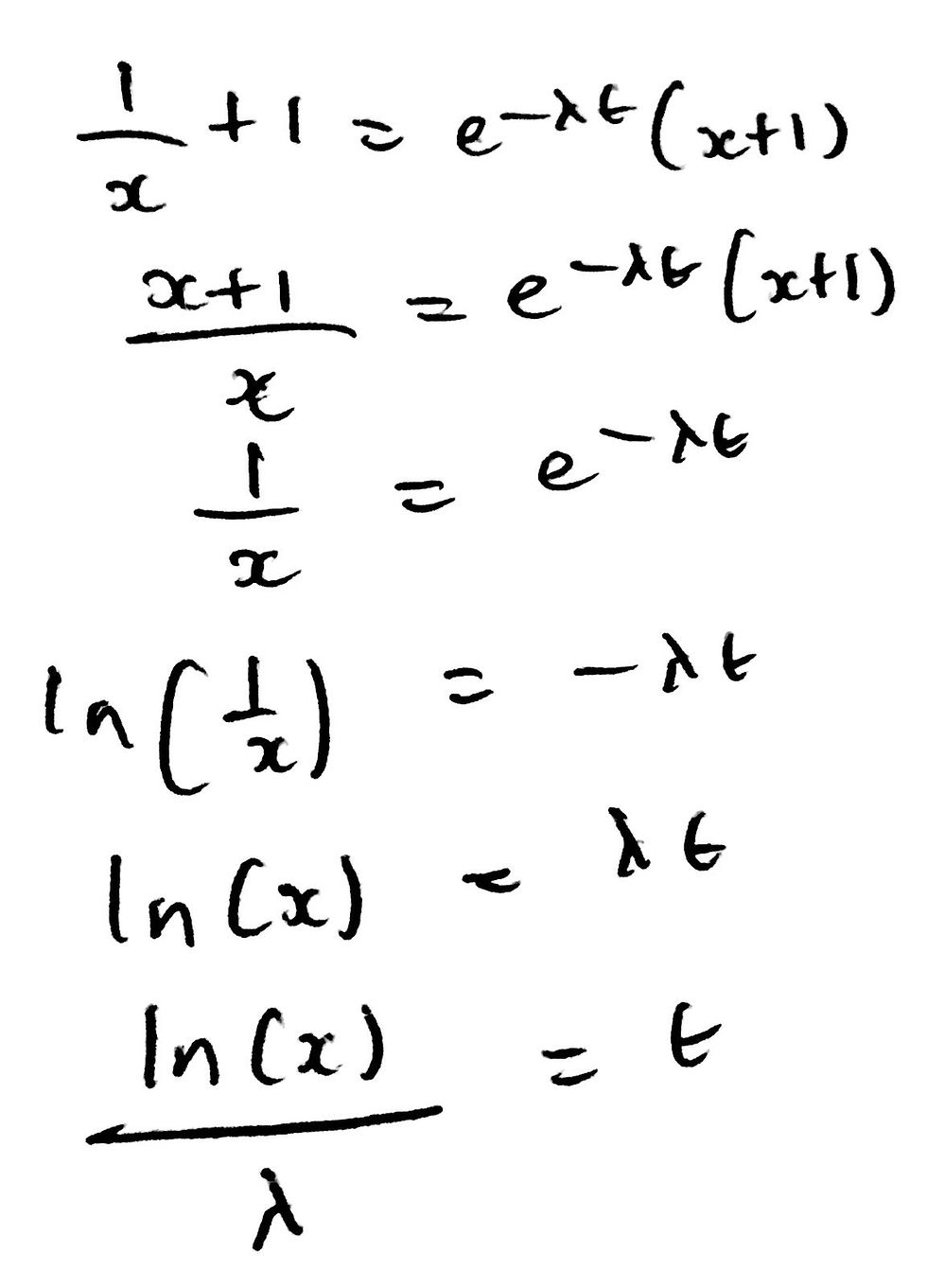
That is it for question 14. It was quite a tricky question but nothing too bad in my opinion. However, this entire question would earn you 6 marks, which for the PAT, is a lot of marks indeed.
Question 17:

First impressions? Eek - at least for me. This seems like a very challenging question just because of the way the information is presented, and this is a common theme throughout the PAT. Oxford will try and trick you out by presenting the question in such a manner that makes it appear far more difficult than it really is (obviously the questions are still hard but you get the point).
Part a:
This part of the question, which is essentially the question as a whole, essentially asks you to compare the shaded grey area to the area of the entire square. After you have done this, you have to rearrange for the angle θ. So, what can we work out so far?
Firstly, the area of the outer square is pretty simple to work out. The side length of the square is equal to the diameter of the outer circle. So you must just essentially square the diameter of the outer circle (2xR) in order to calculate the area of the outer square (As). Now we just have to look at what other shapes we can calculate the area of. The small grey circle in the middle of the square should be pretty simple too. This is just πR^2. Moreover, we can also calculate the area for the outer circle by using the area of a circle. It should be clear that this results in an area of π*x^2*R^2. I have included an image below of the information that we have so far down below.
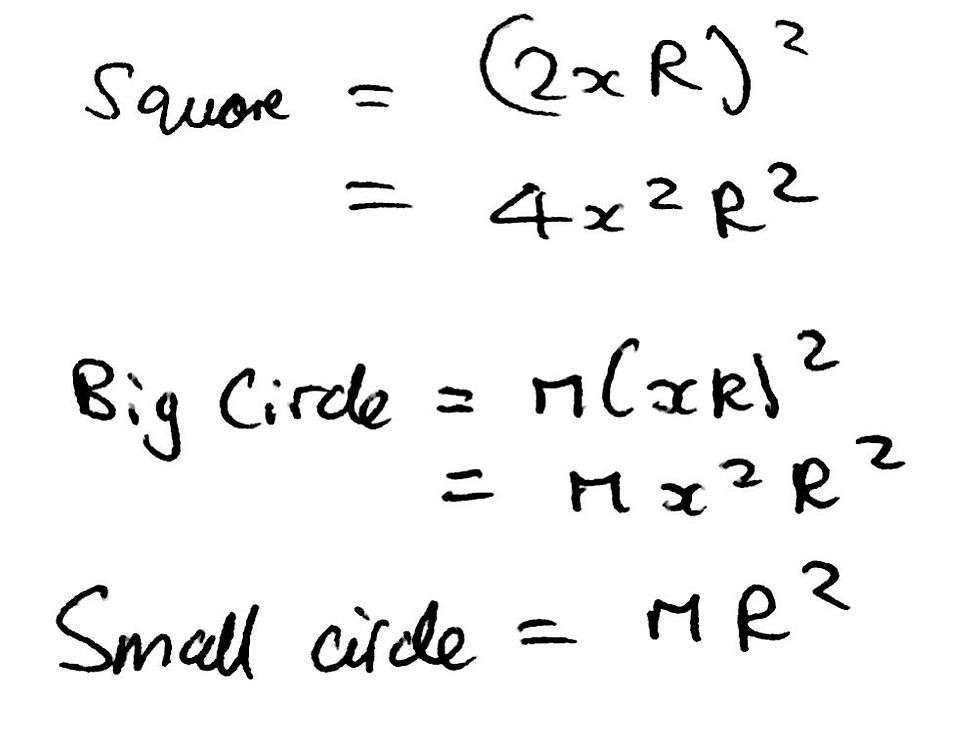
The final piece to this puzzle is calculating the area of an arc sector and then we will be able to rearrange for θ. In order to calculate the ‘missing chunk’ of the outer white circle, we need to calculate the areas of two respective arc sectors. Then, we can subtract the area of the smaller arc sector from the area of the larger arc sector, in order to calculate the area of the ‘missing chunk’. I have shown this in the sketch below for a clearer visual representation.
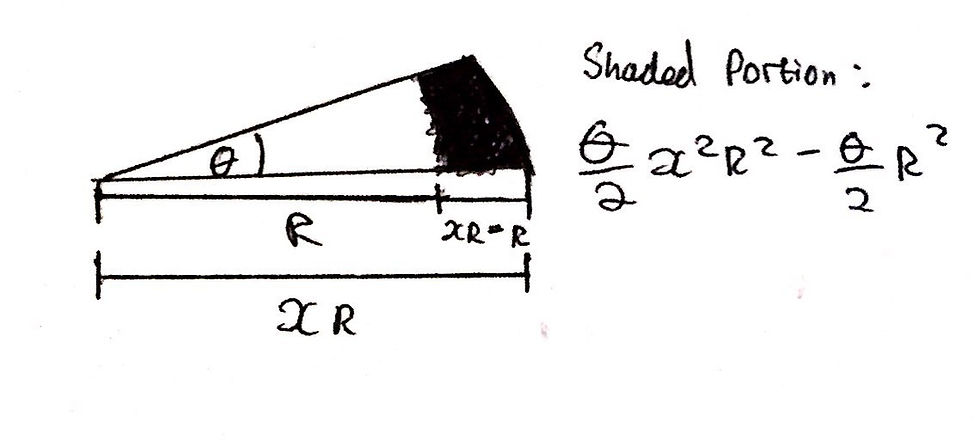
The area of an arc sector is simply (θ/2) * r^2 where r is the radius of that respective arc sector. From here, we can calculate the area of the two respective arc sectors as (θ/2)*x^2*R^2 and (θ/2)*R^2. Using all this information and the fact that the grey area, Ag, is f times the area of the outer square, As, we can create an equation, simplify it, and rearrange it to find a value for θ. I have included an image of my workings below.
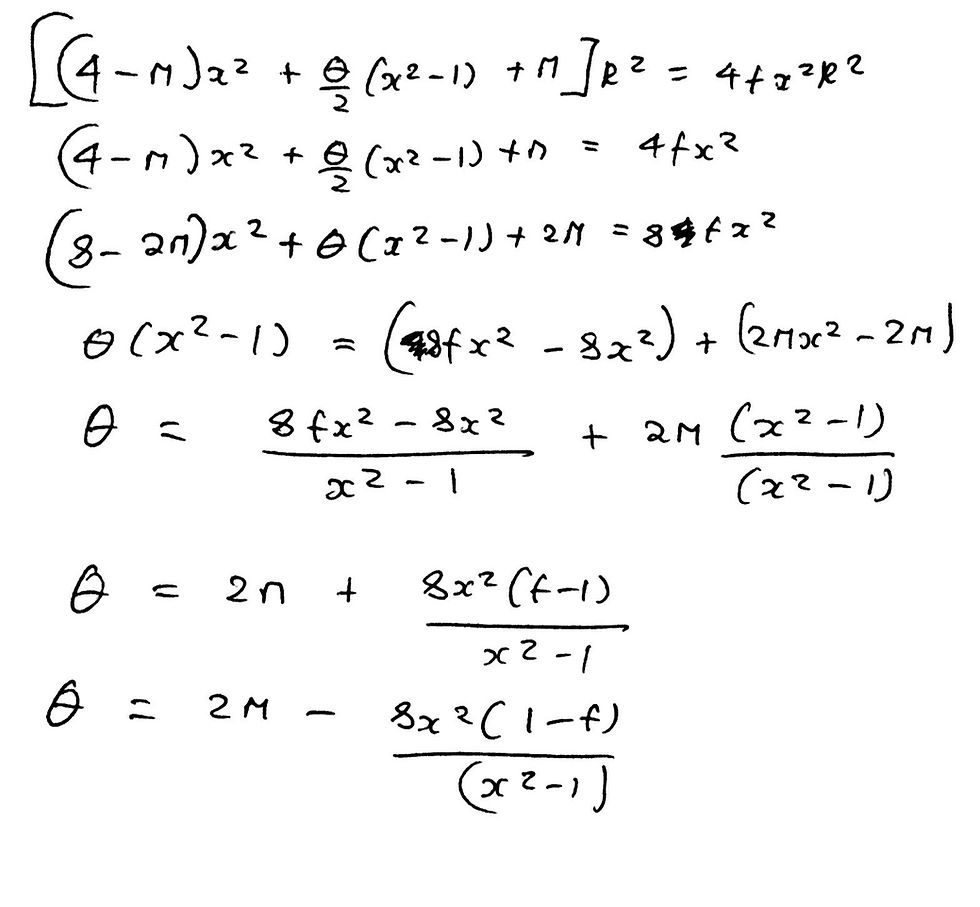
That wasn’t too difficult now was it? Moreover, we have now just earned an extra 6 marks. However, when sitting the actual exam, you would be far more stressed and nervous; therefore, you will most likely be thrown off by the confusing way that the question was presented in. As always, just break down the question into smaller fragments that you can solve. This will then allow you to put all the ‘missing pieces’ of the puzzle together and arrive at the final answer.
Part b:
This part of the question is very simple and straightforward. Just sub in the given values of x and f to calculate a value for θ. Make sure to give your answer to 5 significant figures - many people forget to do this as a result of exam stress.

Question 19:

This question tests the concept of momentum in a very interesting way; the question really stretches your understanding of what the law of conservation of momentum really means.
Part a:
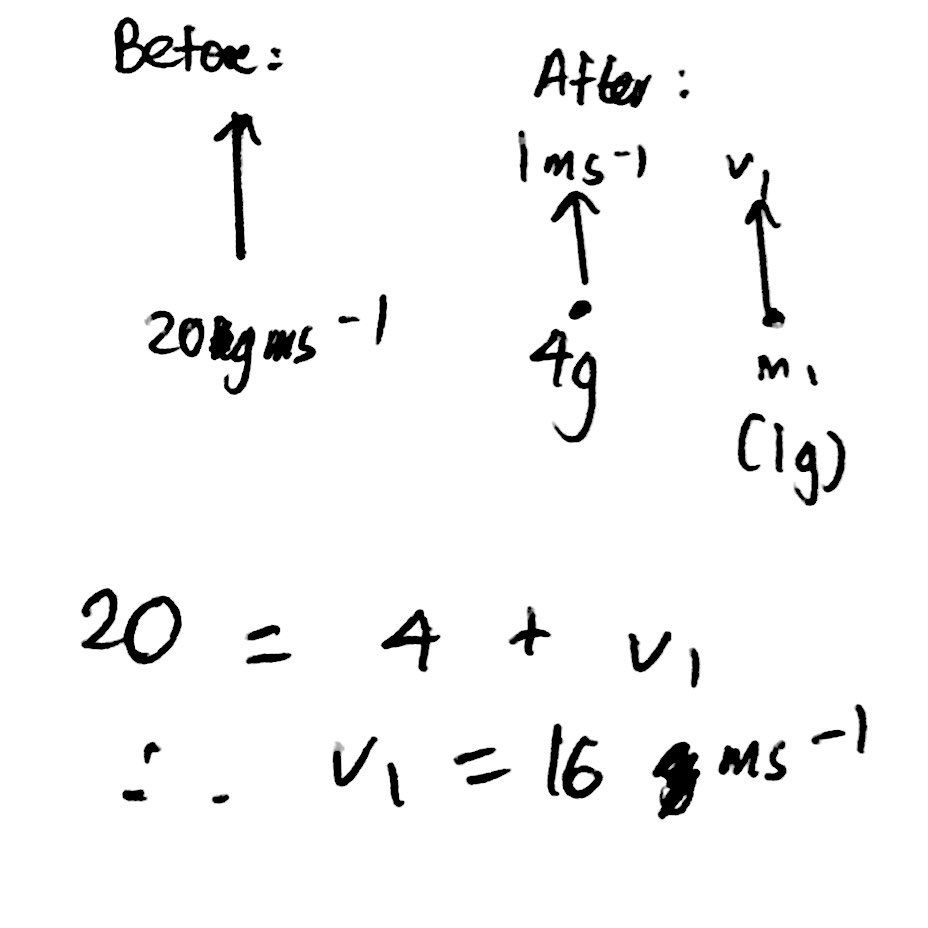
The key to this part of the question is to consider conservation of momentum in two different directions - the vertical and horizontal directions respectively. If we consider the initial state, there is one firework moving upwards with a constant velocity as shown in the diagram below.
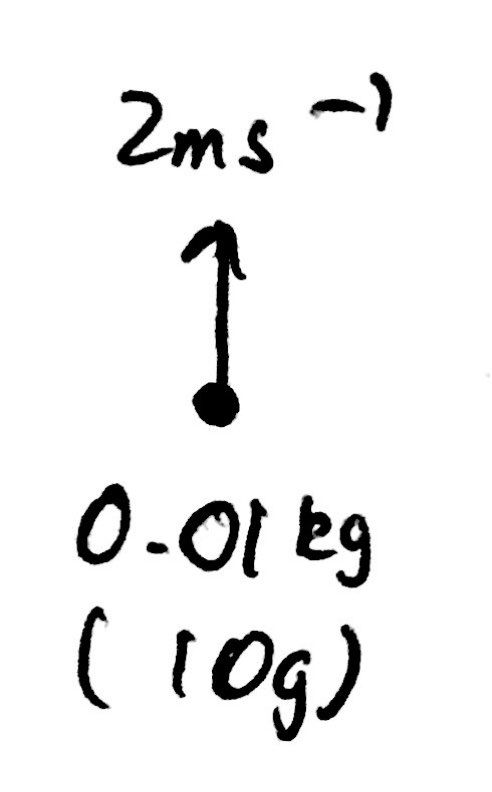
We therefore know that the horizontal momentum must be equal to zero after the explosion. Moreover, we can also calculate what the vertical momentum must be after the explosion as shown in the image below:
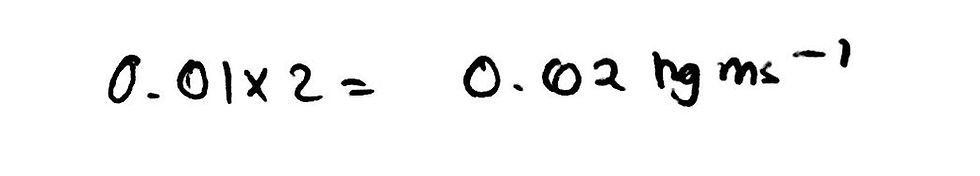
Using this fact and since we are given the value of v4, we are able to calculate the value of v1 as shown in the image below.
Also, in this question, we can use the law of conservation of energy. We know that the firework rocket has an initial quantity of kinetic energy as well as the 1 J of energy that is released in the explosion. We can thus assume - as remember we treat such questions in a so-called ‘physics bubble’ - that this total initial energy is all transferred into the respective kinetic energies of the four pieces of the firework rocket after the explosion. This allows us to set up our first equation in terms of v2 and v3 as shown below.
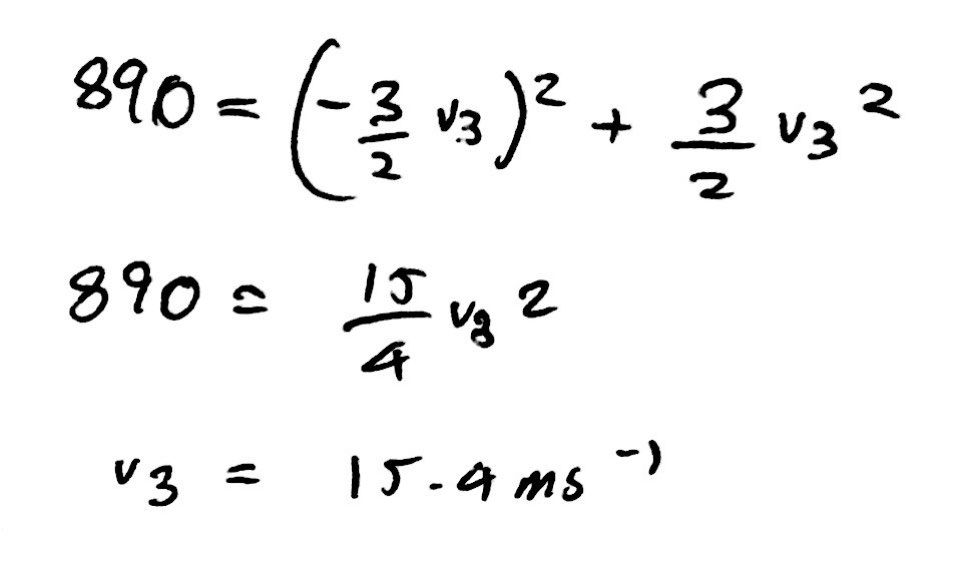
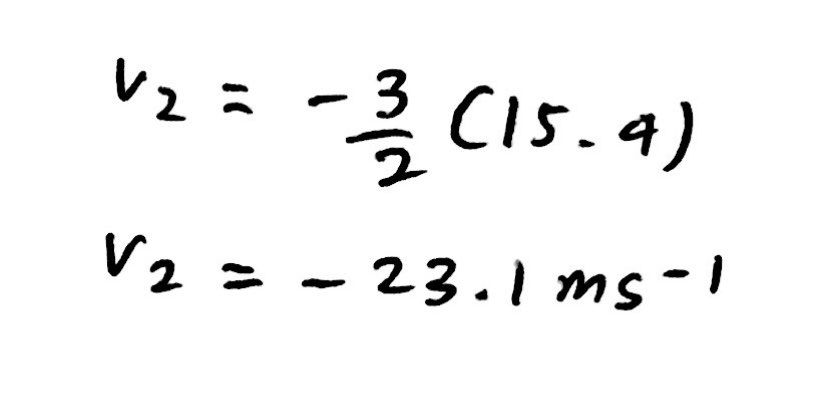
Moreover, by analysing the initial state of the firework rocket before the explosion, we can determine that the total horizontal momentum of the system must be equal to zero after the explosion. This allows us to form a second equation in terms of v2 and v3. Therefore, we can use the system of two equations to solve for v2 and v3, completing this part of the question as we have found every respective speed. Notice that the question asks for the speeds of the pieces and thus the value(s) have no direction as otherwise we would be stating the velocities.
Part b:
This second, and final, part of the question is very intriguing as it requires an intuitive answer. The system as a whole only has a vertical upward momentum as we have previously discussed. Thus, in order for a piece to achieve a maximum speed, the respective piece must be configured in the vertical direction. Now, we just have to decide which pieces must fit where. If m2, m3, m4 were all travelling downwards, they would form a total downwards momentum. However, the entire system - according to the conservation of momentum - is supposed to only have a vertical momentum of 20 kgms-1 in the upwards direction. Thus, the remaining piece, m1, must be travelling at a sufficient speed in the upwards direction to ensure that the system overall has a vertical momentum of 20 kgms-1. The reason why I chose m1 is because it has the lowest mass and thus must have the highest speed for a certain momentum. Thus, our answer for this question could be a brief sketch like follows.
Such a configuration will ensure that one of the pieces, m1 in this case, will be travelling at the highest speed permitted in accordance to the conservation of momentum.
Question 21:

As far as Oxford PAT questions go, this has got to be one of the most confusing questions to understand and that is the whole point of such a question. Questions like this are meant to make you panic and believe that the problem is using some complex electronics knowledge or something of the sorts. However, stay calm and realise that the vast majority of Oxford PAT questions just require some logical reasoning and sometimes a few physics questions. The test is hard, but it doesn’t require any information that you don’t already know.
Part a:
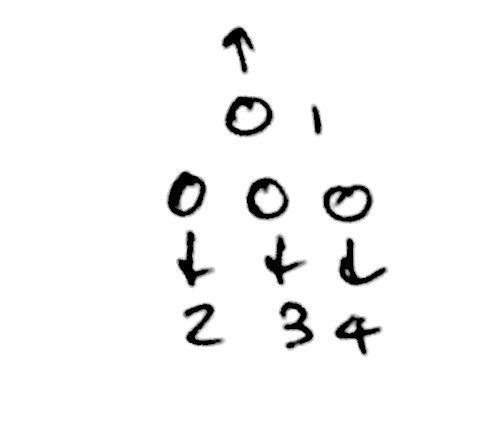
As long as you can roughly understand the general basis of the problem, you should be able to figure out that each of n segments has a minimum delay l, so we can write the following expression.
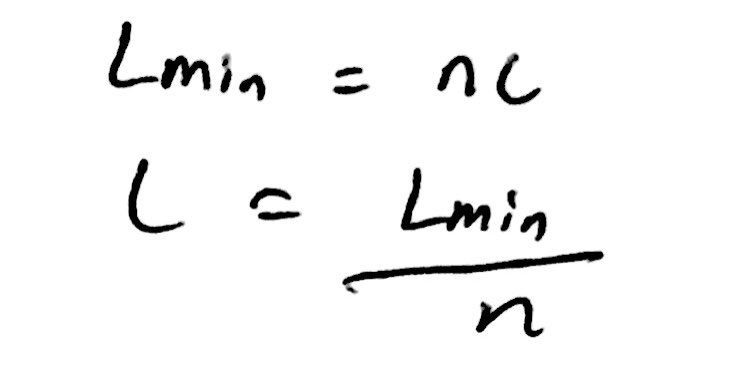
That was fairly simple as it was only a one mark question.
Part b:
The system of delays relies on switches turning on and off - this is effectively, therefore, a binary system. In any binary system, things can either be turned on or off, as is in the case for this delay line system. There are 2^n different states that the switches can actually be in, thus having 2^n delays is definitely the best possible case.
Therefore, the delay increases by a power of 2 with each unit, allowing us to create the following equation.
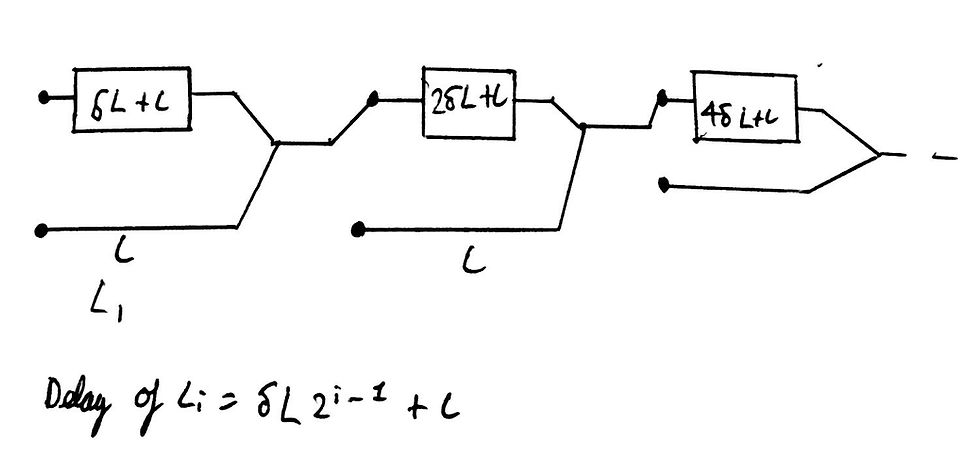
Part c:
We know that this is the smallest n possible that can achieve a delay range ΔL with a resolution of 𝛿L by the binary argument that we made for part b. From here, we can just use algebraic manipulation and logarithms to create an expression for n. Note that the value of n has to be rounded up to the next integer as we must have integer value of n segments.

If you are still confused, even after seeing this explanation, don’t worry; it’s a bit of a weird question. In fact, in pretty much every PAT, there will be a similar “weird” question that you cannot really prepare for. If you are taking the exam, just relax and try your best - remember, you don’t need to get 100% in order to get an interview nor to actually get accepted into Oxford.
Question 22:
Okay, so this question is purely a mathematical question. Therefore, we don’t have to worry about any physics equations. However, we do need to recall the formula for the volume of a cone. I have included an image of the formula below.
This just goes to show how important memorising your formulae is for such admissions tests. Let’s begin to answer this question then. If we imagine that the smaller cone has a diameter d, we can calculate expressions for the volume of both the larger cone as well as the smaller cone, using our trusted formula shown above. I have included an image of the respective calculations down below.
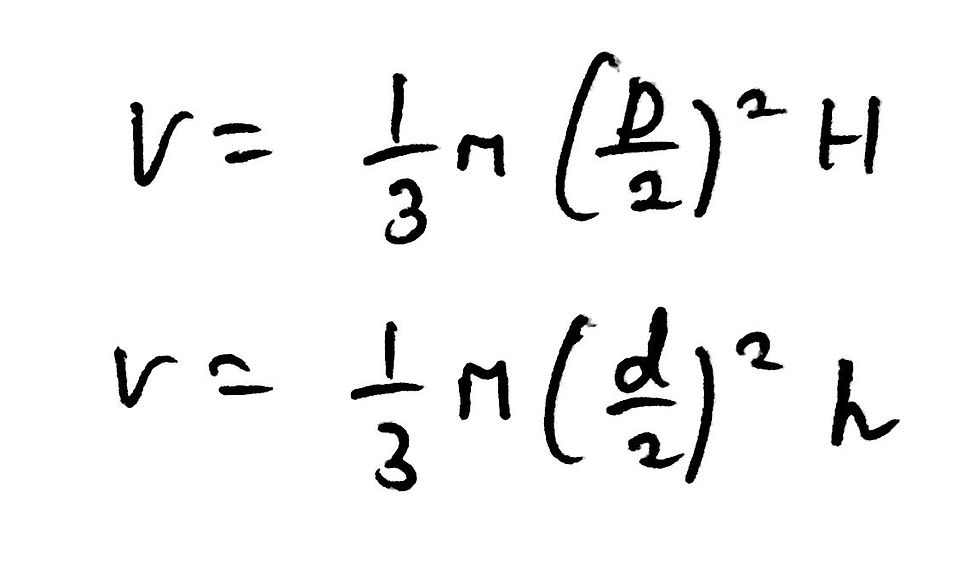
From here, we can also use the fact that the two cones must be similar by definition and thus the ratio of D to H must be identical to the ratio of d to h, allowing us to make the following statement:
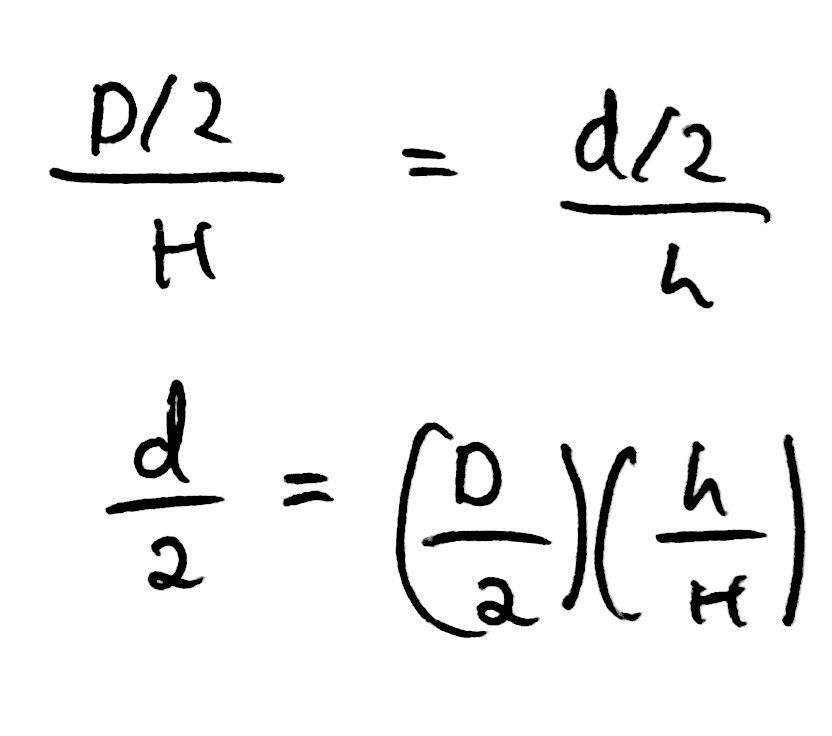
Finally, we can use the fact that the volume of ‘smaller cone’ is V/2 to create an equation. Subsequently, we can then use our ratio relationship to eliminate D and d from the equation, allowing us to write an expression for h only in terms of the dimensions of the cup. This was quite an extensive maths problem but then again it is worth four marks. But, if you think about it, we only used a formula for the volume of a shape, some ratios and a bit of algebra - nothing to be too scared of.
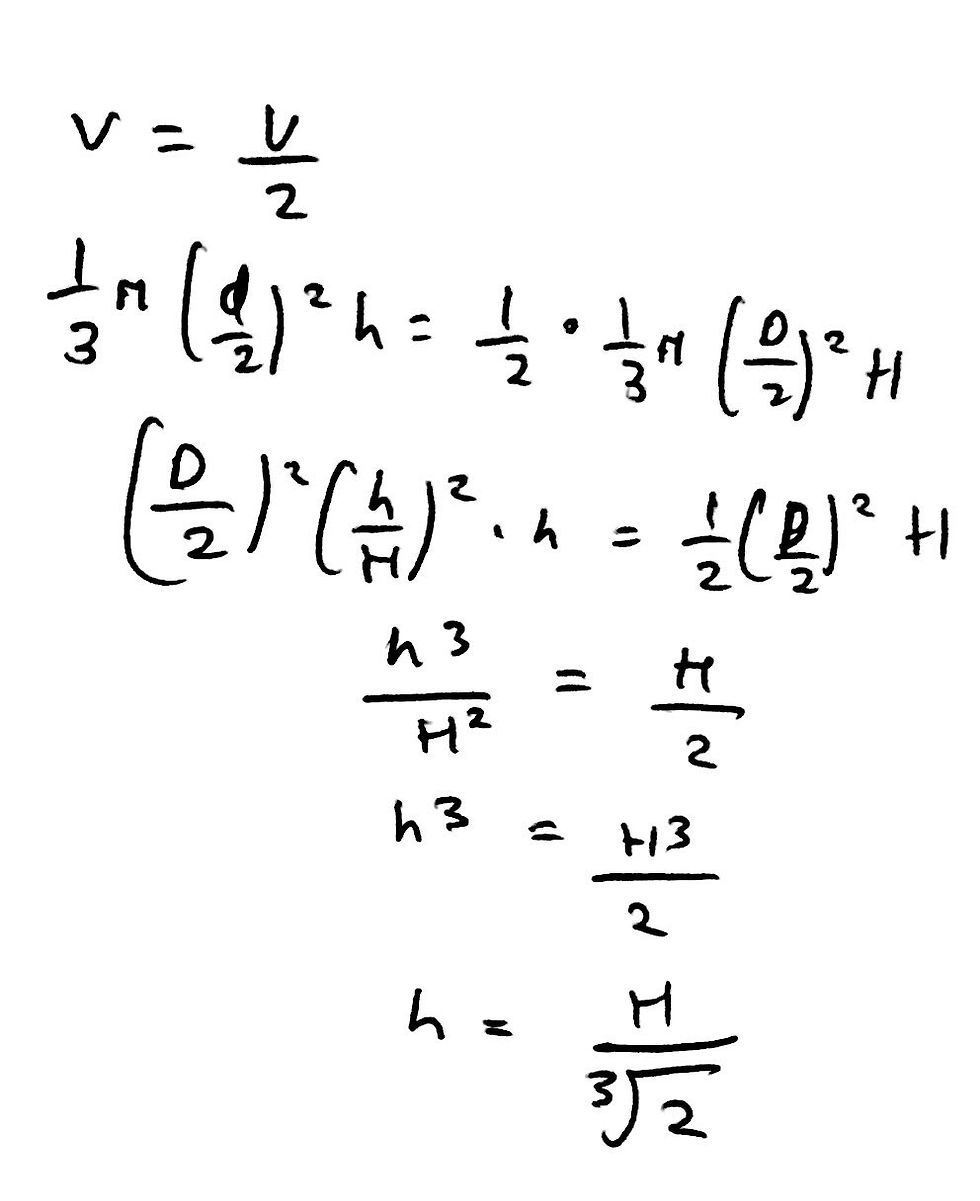
We are finished with question 22, right? No. There is an even quicker way to solve this question - like 15 seconds quick. Every available mark scheme out there (note: Oxford does not publish a mark scheme as they do not want to introduce bias into the solutions) will give you the way I have solved it above, but that is not the way I initially solved it. You see, being the absolute genius that I am (*sarcasm*), I completely forgot the formula for the volume of a cone. But, I remembered something that I learnt all the way back in Year 7 - that is 6th Grade for any Americans reading this.
The super quick solution lies in scale factors. This question fundamentally relies on scale factors. Moreover, there is a very well-known and simple relationship between linear, area, and volume scale factors. It is like follows:

Thus, if the volume of the small cone is V/2 and the volume of the larger cone is V, the volume scale factor must therefore be 2. Thus, the linear scale factor is just the cube root of 2. Ergo, h multiplied by the cube root of 2 is equal to H. We can thus just simply rearrange this to get h as the subject. Et voila! We have the same answer.
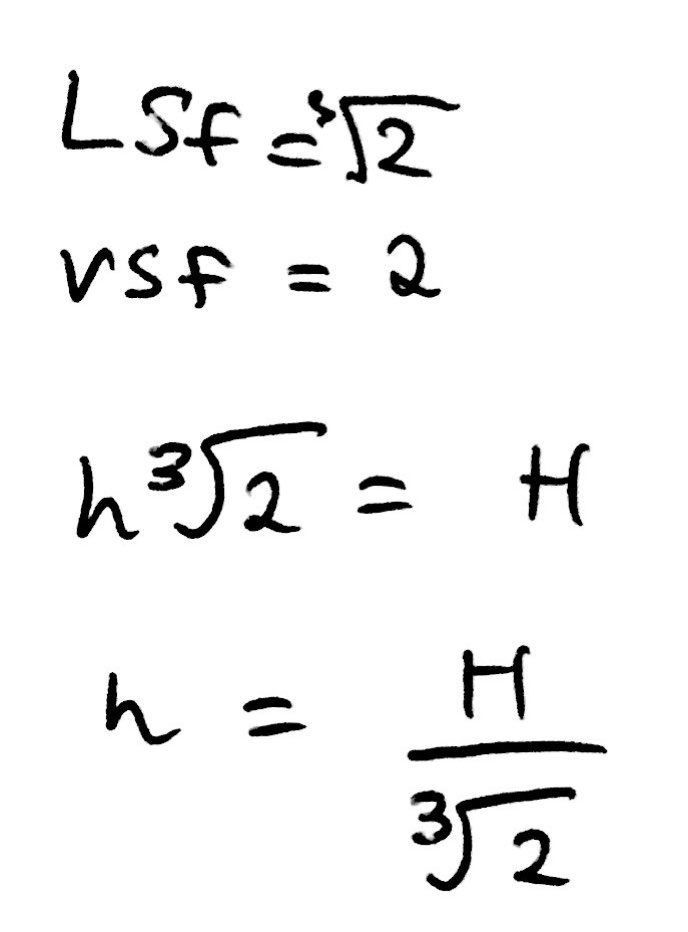
This is why Oxford University right doesn’t release any solutions for its PAT. There are so many neat, little solutions for any maths or physics problem that, if they released solutions, students may be mistaken in believing that there is “one correct” solution, when there isn’t.
Question 24:
This question tests your knowledge of circular motion in a very interesting and challenging way. So, let’s begin by solving the first part.
Part a:
The diagram for this question is very misleading as the actual wording of the question states that the extension is R. Thus, the total length, L, of the spring is equal to R + R0, but the picture makes it seem like the total length is just R, which is not the case.
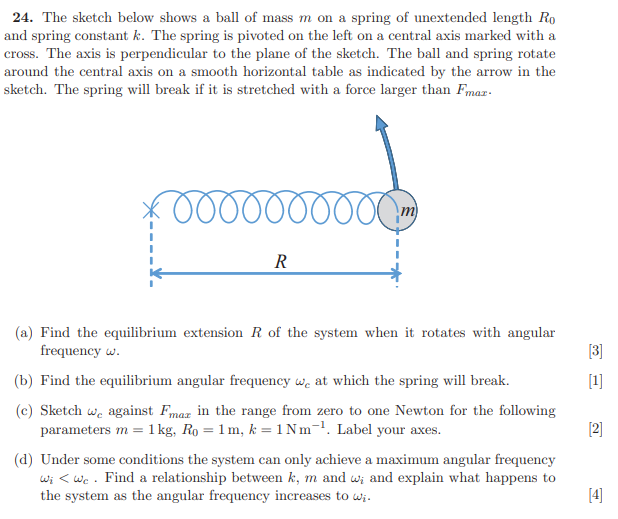
The system is equilibrium in circular motion when the centripetal force is equal to the force exerted on the extended spring. Thus, we just have to equate the force exerted on the spring to the centripetal force of the system and solve for R. I have included an image below showing how to do this.
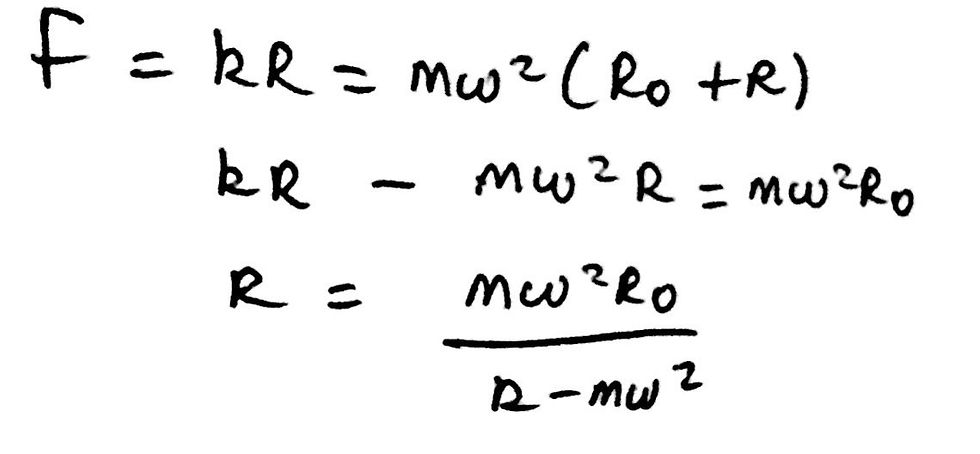
Part b:
The spring will break if it is stretched with a force larger than Fmax. Thus, similar to part a, we just have to equate Fmax to k*Rmax, and substitute in the expression that we have already found for R when answering part a. Remember, this question is only worth one mark and thus it shouldn’t be too complicated. I have included an image below for a visual representation of what I just explained.

Part c:
This is a style of question that you have to get really accustomed to as graph sketching problems are really common in any admissions test. Using our equation for the critical angular frequency (ωc) that we derived in part b, we can substitute in the given values. This allows us to further simplify the equation like so.

Now, you may be looking at that and be confused as to how you could possibly sketch the graph. Well, the easiest method of doing so is to just look at the proportionality relationship between the two variables. In this case, the two variables are ωc (acting as the y variable) and Fmax (acting as the x variable), and the relationship is a square root relationship. If you know the general shape of a ‘square root’ graph, you should be able to easily answer this question.
If you don’t, you can still figure it out by seeing what happens to the value of ωc as Fmax tends towards infinity. It should be clear from the equation that if Fmax were to tend towards infinity the square root would approach closer and closer to 1. In other words, there is a horizontal asymptote at ωc = 1. Thus, we can now sketch the graph as seen in the image below.

Part d:
This is a 4 mark question as it really requires you to have a good understanding of what is actually occurring in this question. If we look back at our equation for the extension of the spring that we derived in part a, we can see that the equation begins to diverge when the denominator is equal to 0. Thus, if we equate the denominator to zero, we can rearrange the equation to get ωi as the subject. If we do so, we get the following equation:
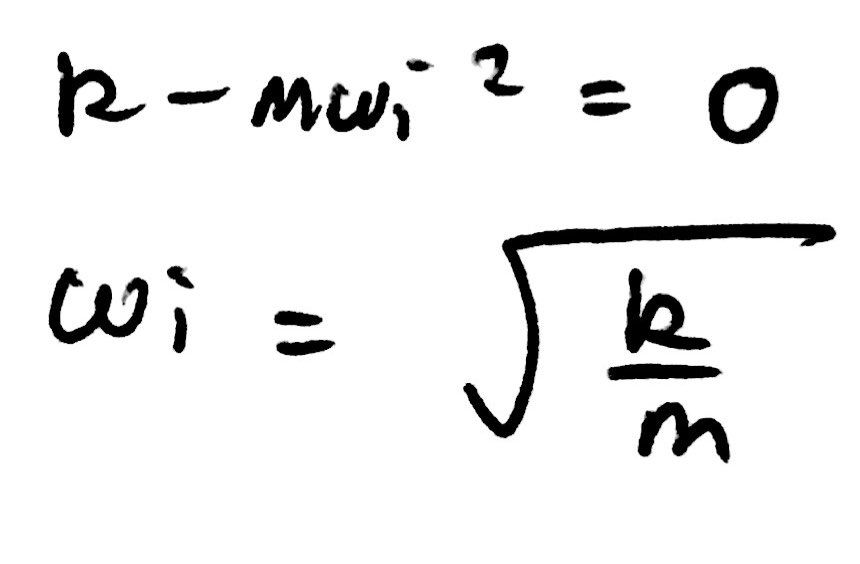
If you have covered simple harmonic motion (SHM), you should be aware that this is the natural frequency of the spring. The system can therefore rotate in circular motion with increasing R until ωi is reached. Beyond this, the spring cannot provide enough centripetal force to keep the mass in circular motion.
For a 4 mark question, relative to some of the other 2-3 mark questions, there wasn’t too much work that needed to be done. That being said, however, this question did require a very good understanding of the actual physics behind the question rather than just simply manipulating the maths side of things.
That is it for this post! I hope that you enjoyed it and learnt a lot from it. I wish you the best of luck in November if you are sitting the PAT. Feel free to leave any questions down below in the comments. Also, remember to join the OnlyPhysics community if you haven’t already for some free perks, such as free online 24/7 help. ‘Till next time; bye!



Comments