MIT Problem Set 2 - Newton's Laws Question 1
- Joel Runevic

- Jun 15, 2020
- 3 min read
What is this?
Massachusetts Institute of Technology (MIT) have released courses, which are available to the public, along with some assignments. These are all aimed at the undergraduate level. The assignments can be found here: https://ocw.mit.edu/courses/physics/8-01sc-classical-mechanics-fall-2016/assignments/ I decided to complete Problem Set 2 as I wanted to challenge myself with more challenging topics that involve Newton's Laws of Motion. I couldn't find an official/unofficial mark scheme and thus decided to post my workings.
Note: I do not recommend simply copying these answers but rather I strongly suggest for you to tackle these problems as long as possible and use my workings as a last resort - I cannot guarantee that they are correct as I completed them independently. I will be uploading solutions to each question separately, with this post introducing the subsequent posts as well as tackling the first question.
Question 1: Stacked Blocks
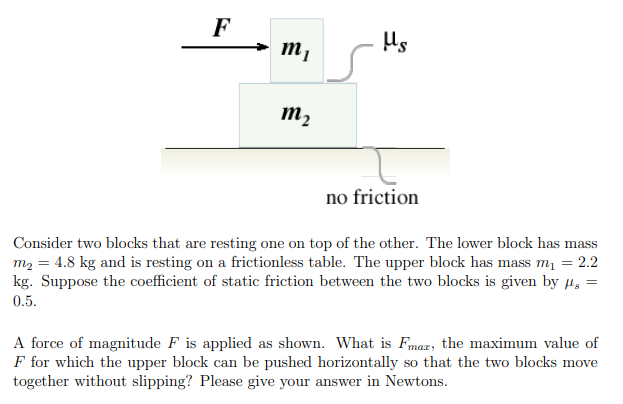
Image sourced: https://ocw.mit.edu/courses/physics/8-01sc-classical-mechanics-fall-2016/assignments/MIT8_01F16_pset2.pdf
Theoretical Analysis:
This question acts a warm-up to the rest of the problem set. If you have studied high-school physics, this problem should be relatively straightforward. As mentioned in the question, the only frictional force acting on the system is between the surfaces of m1 and m2.
It is important to know that friction is always a resistive force, and thus it always acts in the opposite direction to an object's motion in order to oppose that motion. We also must recall that the equation giving the maximum frictional value on an object is F = μN, where F represents the magnitude of the frictional force, μ is the coefficient of static friction, and N is the normal reaction force. Note that F is just convention and does not refer to the force, F, that is pushing the upper block.
Now, as always, we must construct our free-body force diagram, focusing on the upper block. We are already given one force labelled in the right direction and that is F - the force that is applied to the upper block. In the opposite direction is our frictional force, which I will label as μN.
All that is missing is our normal reaction force, N, acting upwards and the weight of m1 acting vertically downwards (m1g). I have included an image of my free-body force diagram below:
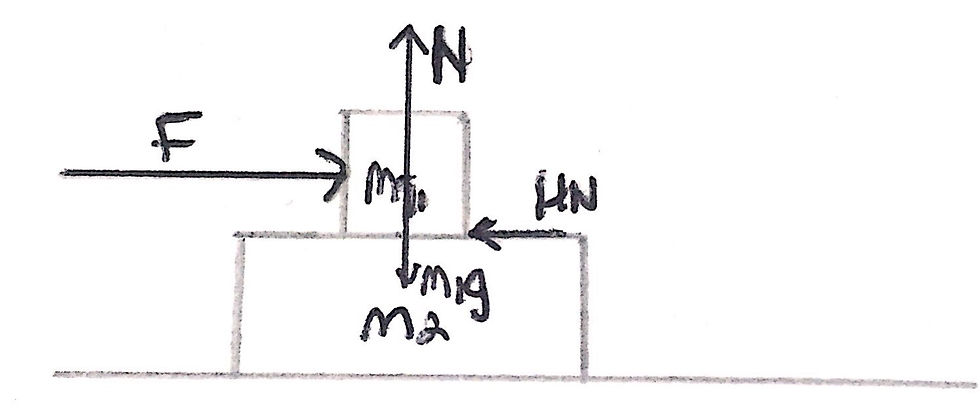
Since m1 is not accelerating upwards, the vertical resultant force acting on m1 should be equal to zero. Therefore, the normal reaction force, N, between the surface of m1 and m2 should be equal to m1*g - the weight of m1.
So, we now have the value of N, and we are given the value of μ in the question (it is 0.5). Consequently, we are able to calculate the maximum frictional force that can be exerted between the two blocks - 2.2 (mass of m1) * 9.81 (value of g to 2 d.p.) * 0.5 (coefficient of static friction) giving 10.8 N to 3 significant figures - I have included an image of my workings below:
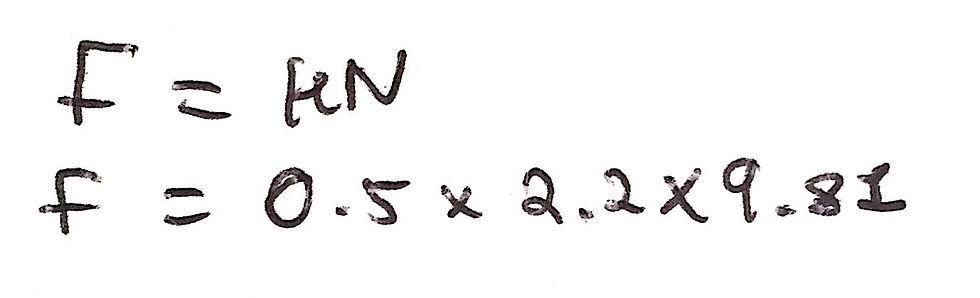
This comes out to 10.791 N which is 10.8 N to 1 decimal place / 3 significant figures.
This is thus equal to Fmax, the maximum value of F for which the upper block can be pushed horizontally so that the two blocks move together without slipping. If the value of F is less than or equal to the maximum frictional force, the force, F, will be opposed by the frictional force. Therefore, both blocks will move together at a constant velocity.
To think about this intuitively, you can imagine that the frictional force is like an adhesive keeping the two blocks together, and thus they move together (this is not actually correct but is a good analogy for one to understand what is going on). However, once the value of F becomes greater than the maximum frictional force, the mass m1 begins to accelerate, causing the upper block to slip and the two blocks no longer move together as a system - in effect, the adhesive force has now been overcome. This analogy works as there is no friction between m2 and the floor.
That is it for question one. If you have any questions about the problem, feel free to comment down below or email us on the Contact Us page. Stay tuned for solutions to be posted on the other questions!



Comments