MIT Problem Set 2 - Newton's Laws Question 2
- Joel Runevic

- Jun 22, 2020
- 6 min read
Question 2: Accelerating Truck and Suspended Bucket
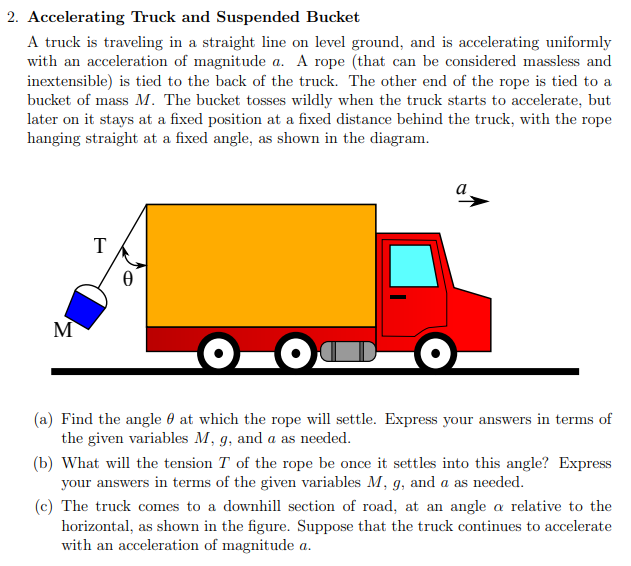
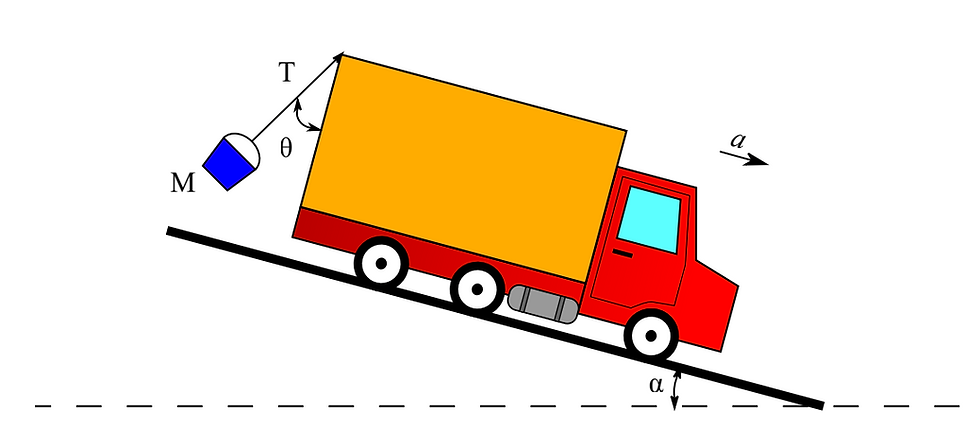

Image sourced: https://ocw.mit.edu/courses/physics/8-01sc-classical-mechanics-fall-2016/assignments/MIT8_01F16_pset2.pdf
Theoretical Analysis:
Question 2a:
This question is more involved than the first question that we tackled, but it is still 'only' uses high-school maths and physics. The common mistake that people make is that they try to incorporate the truck into their answers. They try to add the mass of the truck into their workings or create any other variables that they can think of. However, the key thing to note is that all the variables given in the question part are the variables that we can use in our answer. This should be a very clear indicator that we don't have to worry about the mass of the truck or any variables regarding the truck in fact. The only thing that we have to be concerned about is the truck and the bucket that is attached to it.
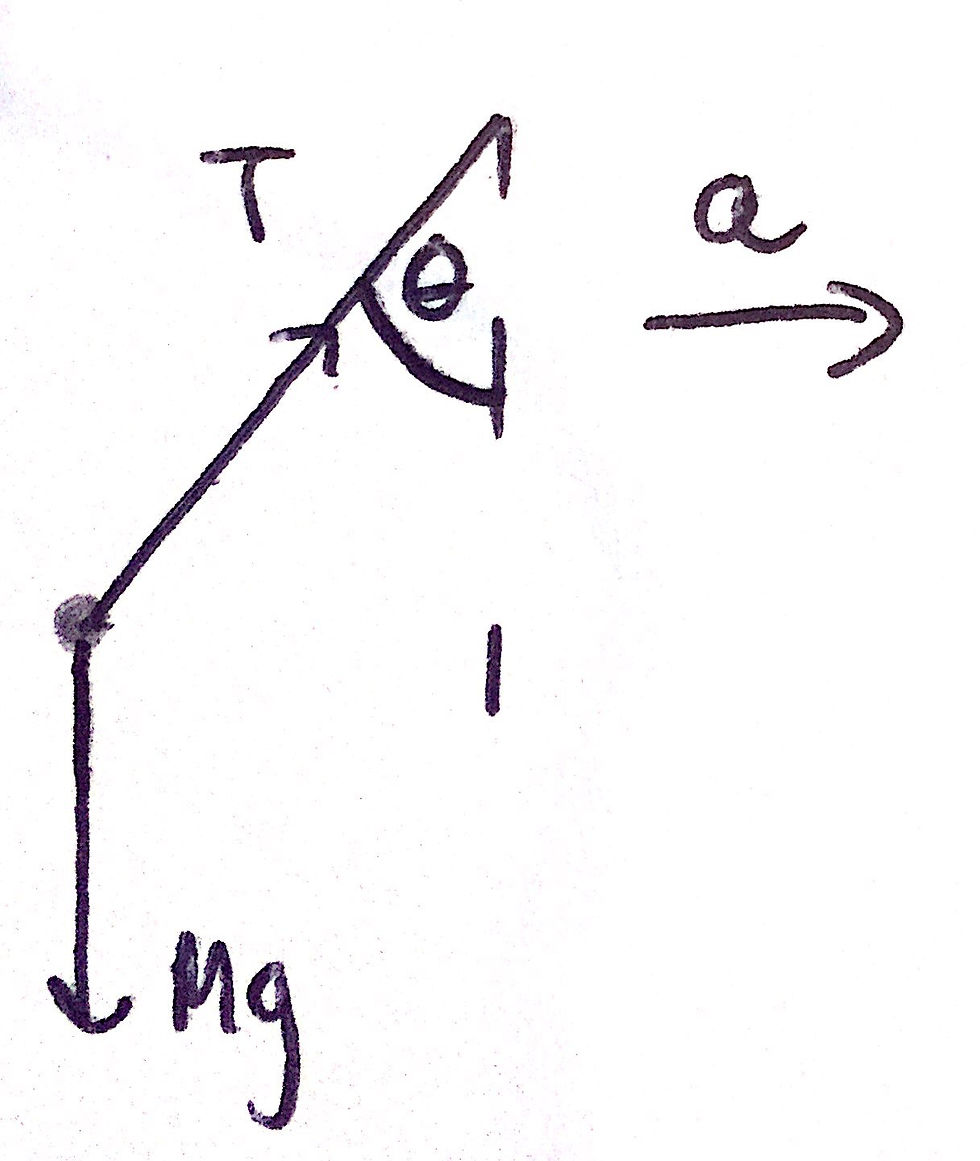
Let's start off by doing a free-body force diagram of the bucket and the rope. It should be clear that the weight of the bucket is assumed to act through the centre of mass and vertically downwards. Now, the rope is at an angle to the horizontal (as shown in the first diagram) and thus has some vertical and horizontal component. The direction of the rope is away from the bucket as shown in my image below. The direction in which tension acts tends to confuse many people. You can always decide in which direction the tension must act by remembering that a rope cannot push an object: it can only pull an object. These are the only two forces that we need to consider for this part of the question. As aforementioned, I have included the free-body force diagram below.
Now, we can begin to actually answer the question. We know that the truck is accelerating uniformly at some acceleration, a. The bucket must be accelerating at the same magnitude, a, as the rope is inextensible and massless (we are given this in the question). If we imagine the bucket being pulled by the rope, it should be clear that it is the horizontal component of the tension that is responsible for providing this horizontal acceleration.
From Newton's Second Law (which is often abbreviated as F=ma - although this is not actually Newton's Second Law but is the simplified version when the mass of an object is constant), we can write that the horizontal component of the tension is equal to the mass of the bucket, M, times its acceleration, a. By using simple trigonometry, you should arrive at the following equation:
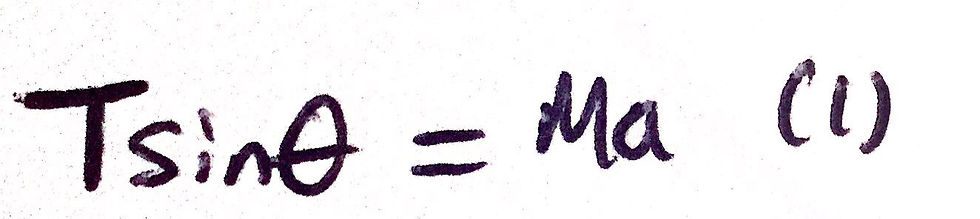
Okay, so we have an equation in which the angle, θ, is on one side. Therefore, we can just simply rearrange for θ, right? Wrong. If you look carefully at the variables that we are allowed to choose from in our answer, the tension in the rope, T, is not there. This is often an indicator that you must develop some sort of second equation that can help you. We can develop this said second equation by just resolving forces vertically. If we do this and consider the vertical components of each force acting on the bucket, and the fact that the bucket is accelerating only in the horizontal direction, it should be clear that the weight of the bucket is equal to the vertical component of the tension in the rope. This gives us the necessary second equation that we needed, as shown below:

We just need to find a way to cancel the Ts. This can be done by utilising a neat, little trick. We can just divide the two equations by each other. In fact, this trick will be used quite often in this question (and other similar questions) as we can cancel out a variable that is not permitted in the final answer - T in this case.
You do, however, need to know a common trigonometric identity, which I have included below:
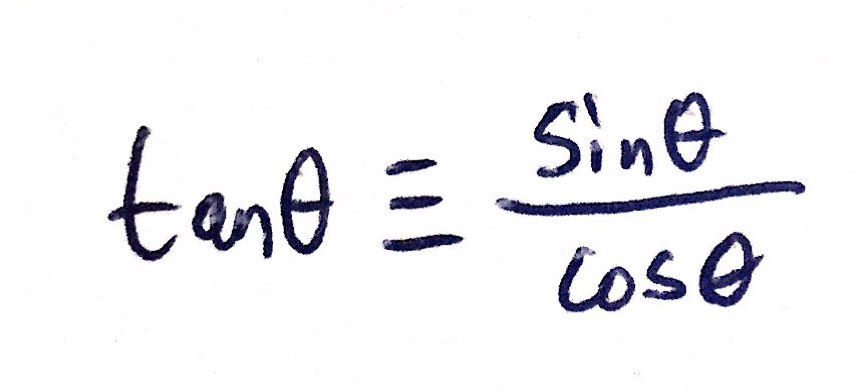
This identity has an origin in simple trigonometry. If you take a right-angled triangle with a hypotenuse of 1 and an angle θ, like I have included below, you can write out the two missing sides as simply cosθ and sinθ respectively - this should be apparent from trigonometry. We know that tanθ is simply the ratio between the side that is opposite to the angle and the side that is adjacent to the angle. In effect, tanθ is equal to opposite/adjacent. In this case, we know the magnitude of the opposite size (sinθ) and the adjacent side (cosθ). Therefore, we know that tanθ is equal to sinθ/cosθ. I have an included a diagram to help visualise this below:

Knowing this handy trigonometric identity, we can divide equation 1 by equation 2 and rearrange the resulting equation to have the angle, θ, as the subject. This has been done in the image below:
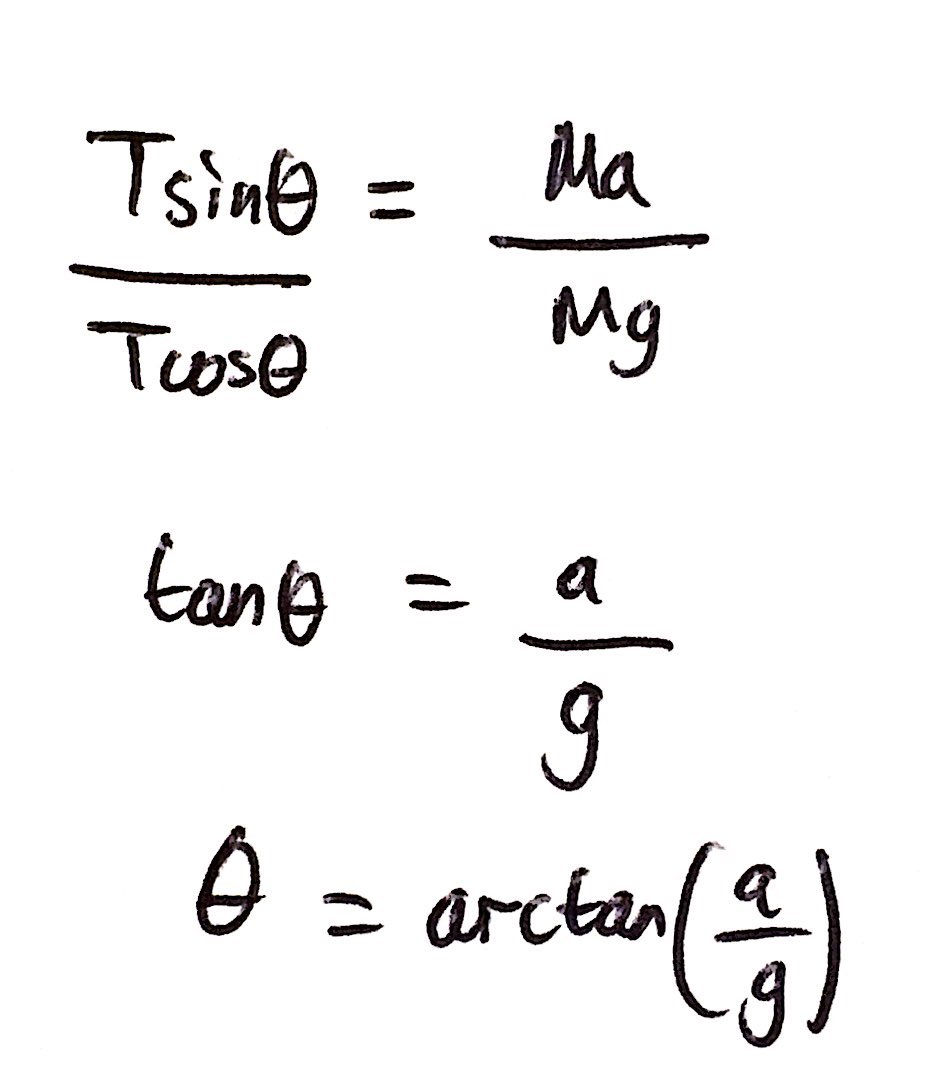
Question 2b:
Notice how there is no mention of θ in any of the variables that we can use in the answer of this part of the question. Therefore, we must somehow eliminate θ from our two equations rather than T.
This is where our second trigonometric identity will come into play. If we take the triangle with hypotenuse 1 that we saw before, we can express the hypotenuse in terms of cosθ and sinθ. This can be done through Pythagoras' theorem. By using the fact that a^2 + b^2 = c^2, we can state that sin^2(θ) + cos^2(θ) = 1. I have included an image to help you visualise this below:
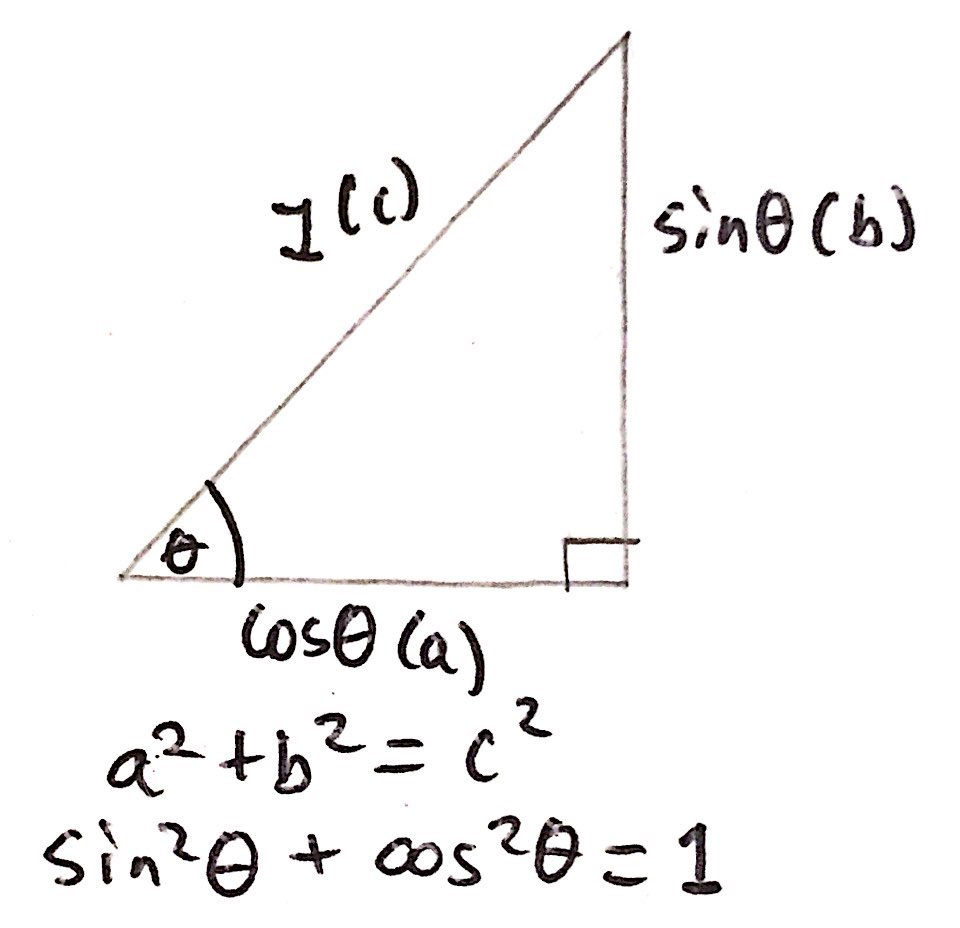
Therefore, if we square both sides of equation 1 and equation 2 and add the two equations together, we can simplify the resulting equation and eliminate the variable θ. This will therefore allow us to have an expression for T in terms of g, a, and M only. I have included an image of the algebraic manipulation required below:
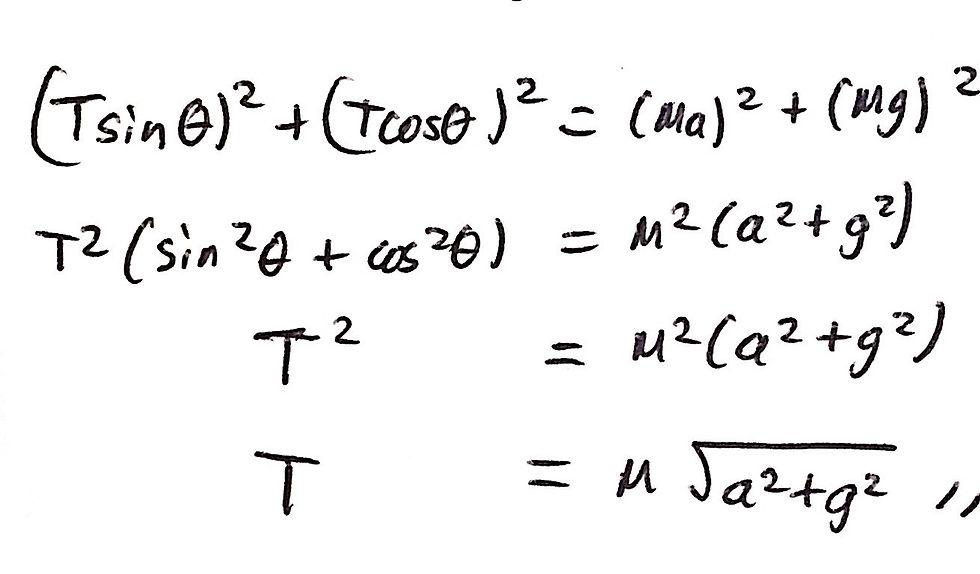
Question 2c:
The next two parts of question 2 are more difficult than parts a and b but expand on the mathematical techniques that we have used so far. The forces acting on the bucket are exactly the same and so are the trigonometric identities that we are going to use. The only difference is that the bucket is at an angle, α, to the horizontal. For simplicity, I will position the bucket, in my free-body force diagram, just hovering ever so slightly above the inclined road. I have included an image of the free-body force diagram below, with the relevant angles shown (they are calculated using simple geometry):

In this scenario, the component of the bucket's weight and the component of the tension in the rope that are parallel to the slope are responsible for the acceleration of the bucket. In effect, this is our new equation 1. The biggest difficulty that one may encounter here is ensuring that they resolve the forces correctly, according to the angles that are provided.
Our second equation will stem from the fact that the component of the bucket's weight that is perpendicular to the slope is equal to the component of tension that is also perpendicular to the slope. The two equations can be shown below:
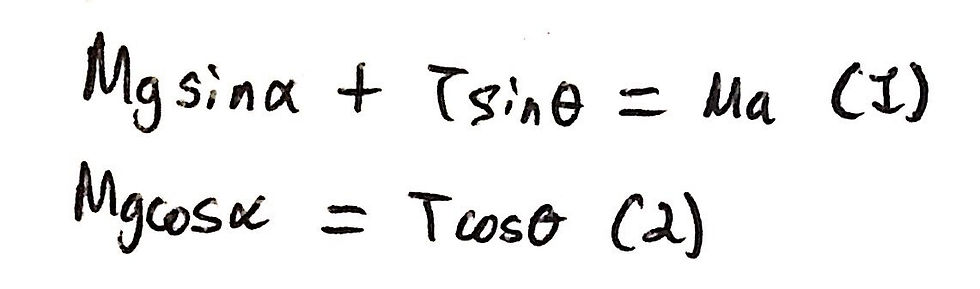
For this question part, we will follow the exact same methodology as part a. In order to arrive with only the angle θ as the subject of the equation, we must divide equation 1 by equation 2 and simplify accordingly. I have included an image of this below:
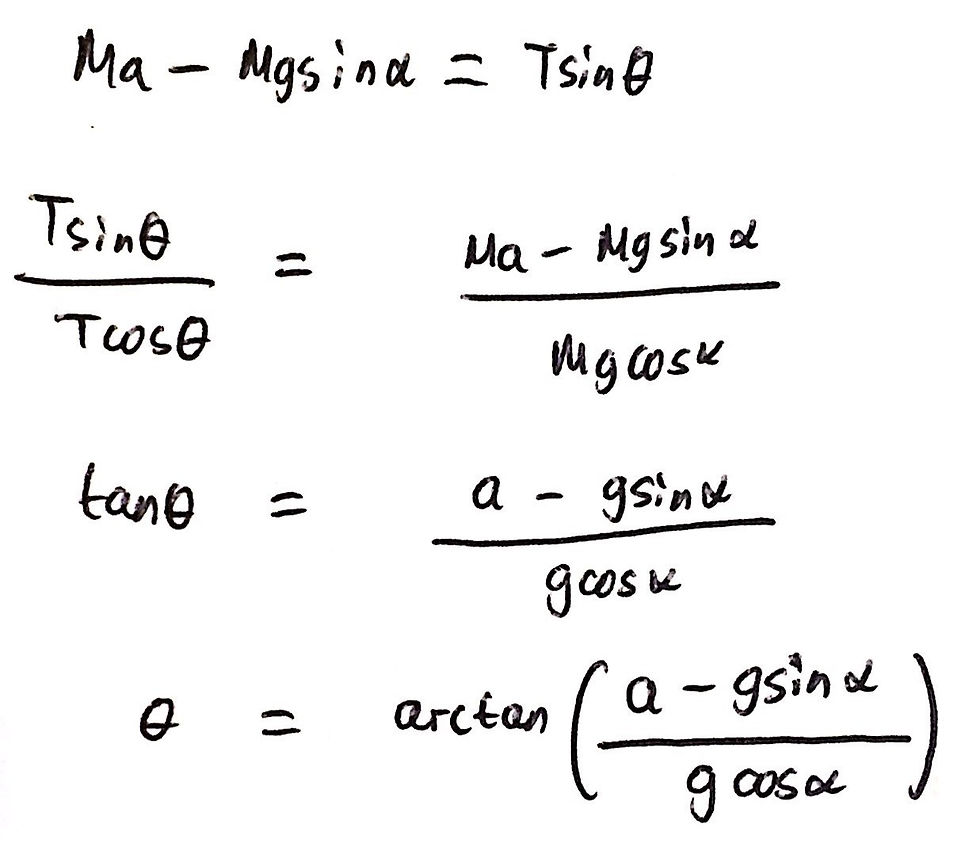
Question 2d:
To answer this part of the question we must utilise the same method as in part b. You may have noticed a pattern here - parts c and d just test what we did in parts a and b, but we just have to consider an inclined, rather than a horizontal, plane.
To do so we just use the second trigonometric trigonometric identity that we derived. Thus, we square both sides of equation 1 and equation 2 and add the two equations together. Subsequently, we just rearrange the resultant equation (this turns out to be quite fiddly and tricky, so be careful), resulting in T being the subject of the equation. Ensure that you have simplified the resulting answer as much as possible. I have included an image of the required algebraic manipulation below:

That is it for question two. If you have any questions about the problem, feel free to comment down below or email us on the Contact Us page. Stay tuned for solutions to be posted on the other questions!



Comments