MIT Problem Set 2 - Newton's Laws Question 3

Question 3: A wedge against a wall

Image sourced: https://ocw.mit.edu/courses/physics/8-01sc-classical-mechanics-fall-2016/assignments/MIT8_01F16_pset2.pdf

Question 3a:

This question is very interesting in the fact that it poses a relatively simple task in a rather peculiar way - in other words, it is not really what you would find on a high-school Physics paper. 'The magnitude of the sum of all forces acting on the box' is really just asking about calculating the result force on the box. As always, we must begin by thinking about what forces act on the box and draw our free-body force diagram.

So what forces do act on the box? Well, we have the weight of the box that acts vertically downwards through the box's centre of mass. This force has magnitude mg. There is no friction between any of the surfaces, so we can ignore any frictional forces. Considering the box is in contact with the inclined surface, there must be a normal reaction force, N, between the surface and the box. This force is always perpendicular to the surface. I have included an image of the free-body force diagram below:

The free-body force diagram.

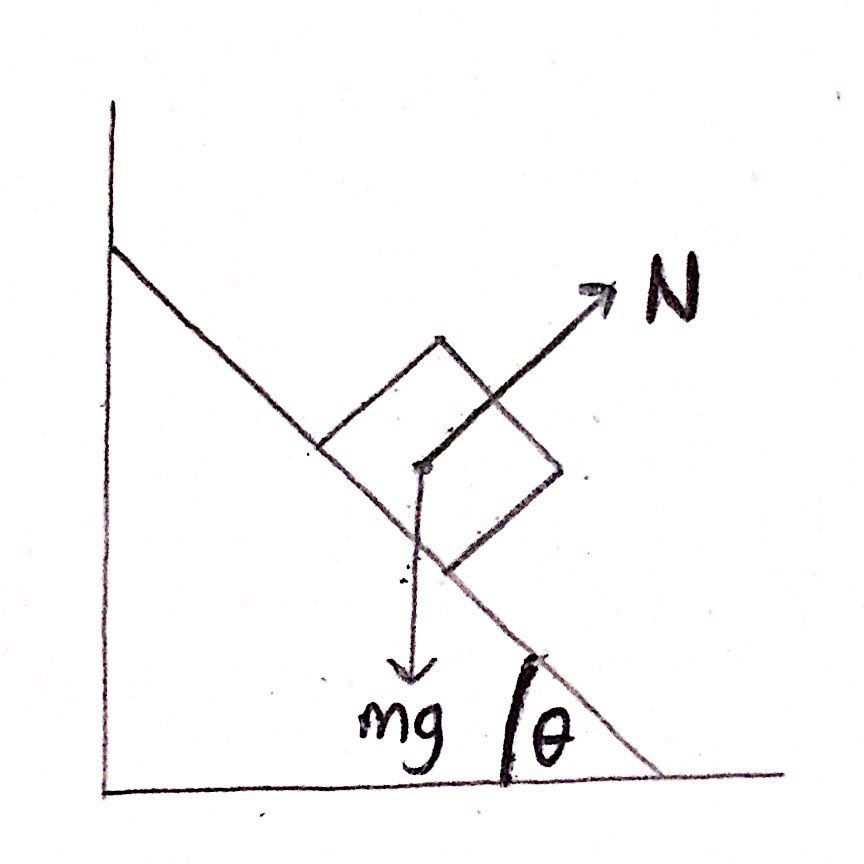
If we think about this more carefully, the component of the box's weight that is perpendicular to the slope is going to be equal in magnitude to the normal reaction force, N, but in the opposite direction. In effect, the weight's perpendicular component will 'balance out' the normal reaction force. Thus, the only force acting on the box that is not 'balanced out' by any other force is the component of the box's weight that is parallel to the slope. The normal reaction force will have no impact on the parallel component of the object's weight as both forces will be perpendicular to each other. This is intuitive as the object is moving down the slope and therefore the resultant force must act in the same direction.

If you resolve the weight of the box correctly you should get the following answer:

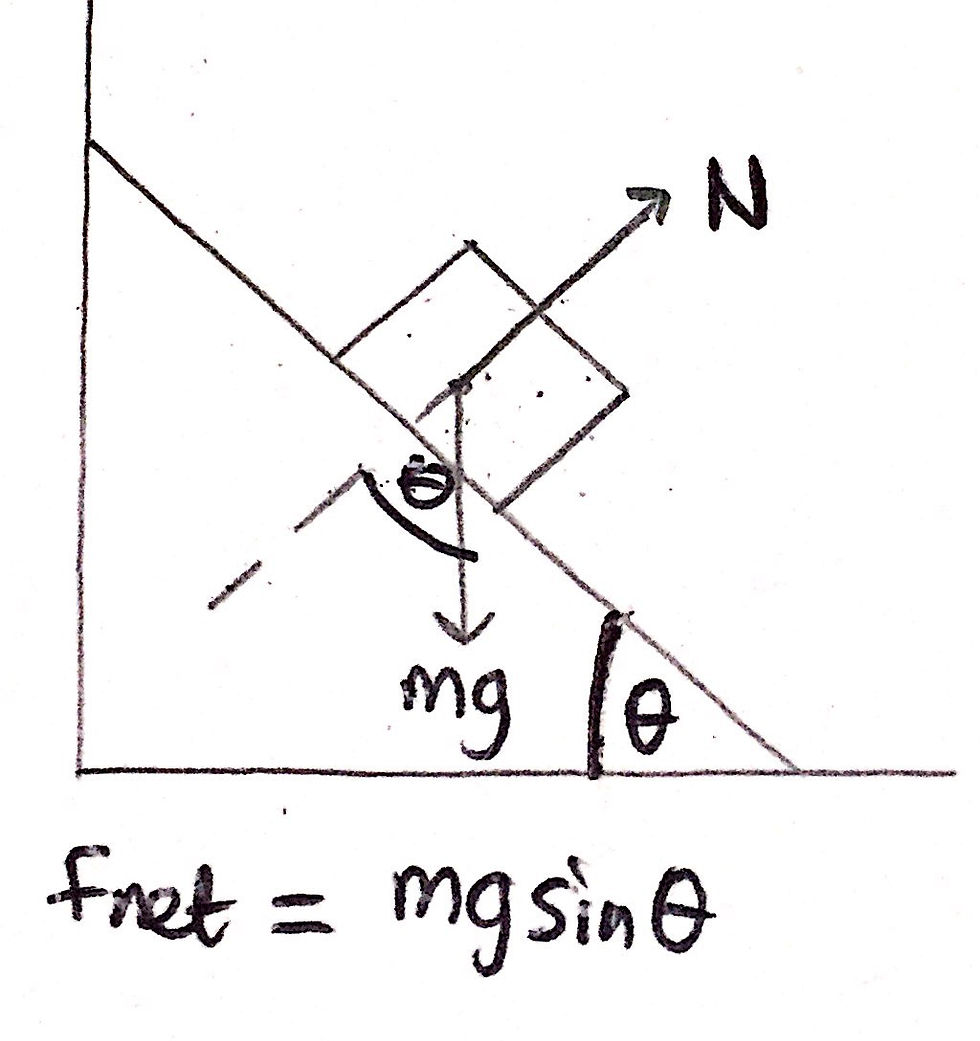
That is it for part a. Easier than it looks, right? Sometimes, with some of these questions, the trickiest step is simplifying the question and trying to really understand what it is that the question is asking you to do. We did that here, and therefore we found the question to be relatively straightforward.

Question 3b:

This part of the question, in my opinion, is a lot harder than part a. Before we begin, we really need to think about what it is that is going on. The resultant force acting on the wedge needs to be equal to zero for the wedge to remain stationary (which, in this case, it does). The normal reaction force between the wedge and the wall will be perpendicular to the point of contact between the wedge and the wall - therefore, it will act directly to the right.

This contact force must be equal and opposite to another force that is acting on the wedge. There are no frictional forces so friction cannot be responsible for this. The only other force that is acting on the wedge is the normal reaction force between the box and the wedge. Therefore, some component of the normal reaction force must be equal in magnitude, but in the opposite direction, to the contact force between the wall and the wedge. We can do this by resolving forces and by utilising a few angle laws. I have included an image of this below:

Another free-body force diagram.

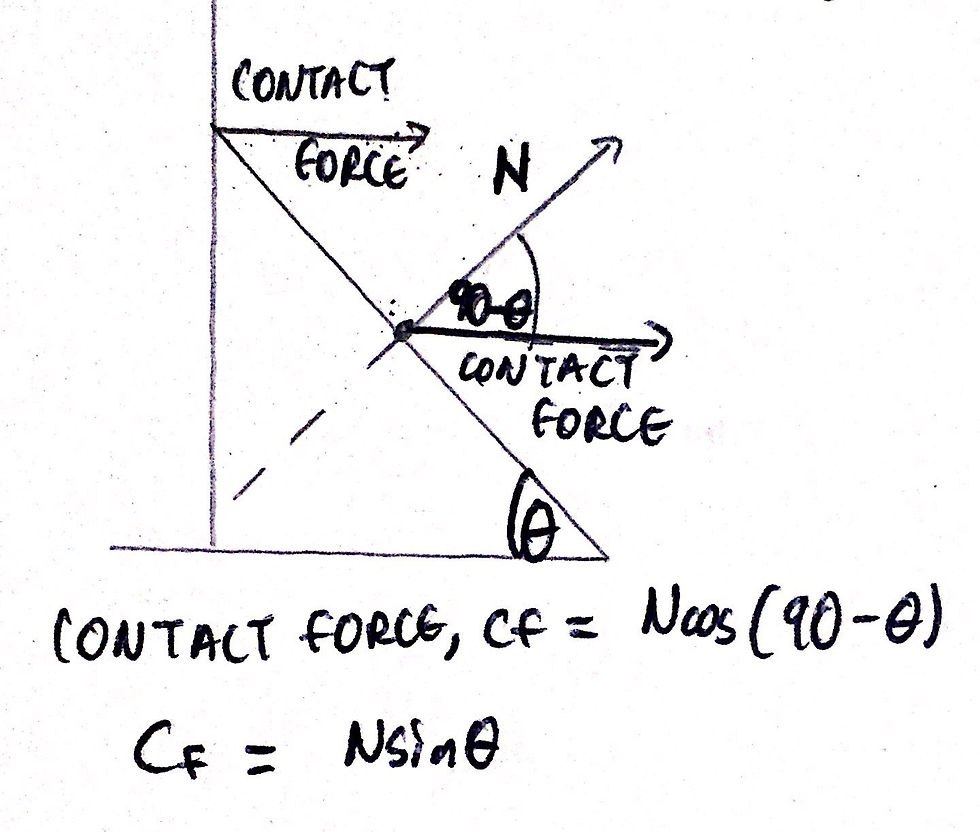
Note: If you look above, I used a neat little trick. Cos(90-θ) is equal to sin(θ) - this can be derived from the cosine subtraction formula which I will include at the bottom if the post if you are interested.

From part a, we know that the component of the weight that is perpendicular to the slope is equal to the normal reaction force. Therefore, we can substitute this into the above equation in order to arrive at our final answer (remember - we cannot use the variable N in our final answer). I have included an image of this below:

Arriving at our final answer.

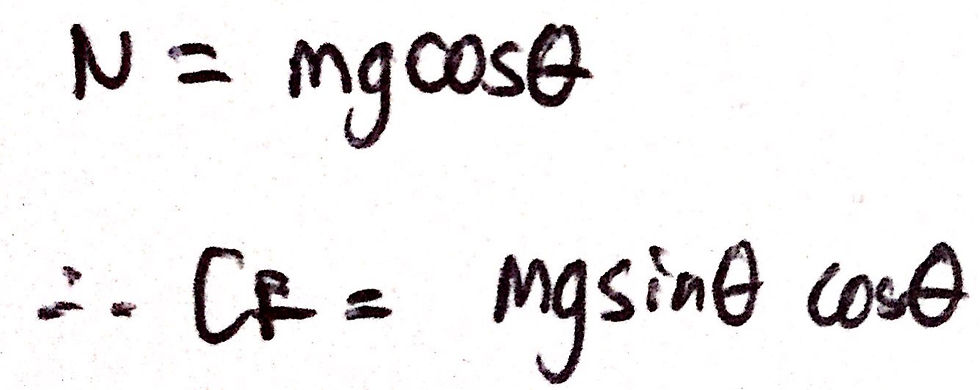
This is our answer! This part of the question involved more thinking and a cool little trick that I showed you before with the relationship between the sine and cosine functions. Speaking of which, I will now quickly derive that relationship so that you can see where it comes from. All you need to be familiar with is the cosine subtraction formula (there is a derivation for this, but it is much longer so I won't be including it here). I have included an image of the derivation below:

Derivation of the fact that cos(90-θ) = sin(θ).

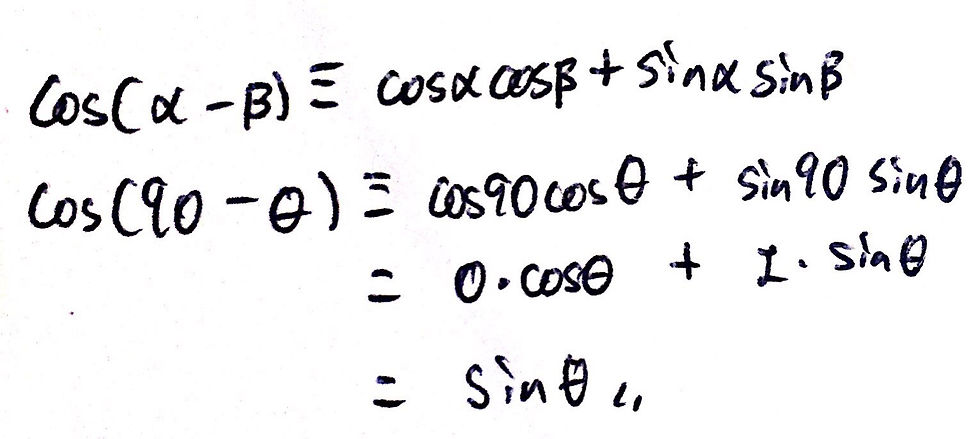
That is it for question three. If you have any questions about the problem, feel free to comment down below or email us on the Contact Us page. Stay tuned for solutions to be posted on the other questions!