MIT Problem Set 2 - Newton's Laws Question 4

Question 4: Dragging two blocks

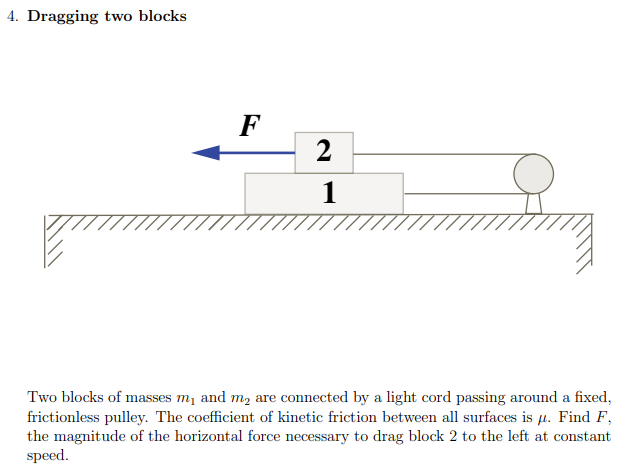
Image sourced: https://ocw.mit.edu/courses/physics/8-01sc-classical-mechanics-fall-2016/assignments/MIT8_01F16_pset2.pdf

Theoretical Analysis:

This question involves several objects that we must consider. As always, let us start by creating a free-body force diagram of what is going on. Firstly, we have two masses, m1 and m2, which will both have their respective weights acting vertically downwards of magnitudes m1g and m2g, respectively. Next, there will be a normal reaction force, which I will label as N1, between Block 1 and the floor, acting vertically upwards. Likewise, there will be another normal reaction force, which I will label as N2, between Block 1 and Block 2, also acting vertically upwards. We are also given an external force, F, that acts to pull Block 2 in the left-hand direction.

The question also informs us that the coefficient of kinetic friction between all surfaces is μ, which therefore implies that there exists frictional forces within this system of objects. However, it is important to note that the pulley is described as both fixed and frictionless, resulting in the light cord having a constant tension - more on this later.

In terms of the frictional forces, it is important to correctly identify the direction in which each respective frictional force will act. In this scenario, there will be two separate frictional forces. One frictional force will exist due to the movement of Block 1 on the surface and the other due to the movement of Block 2 on Block 1 (or vice versa).

In order to determine the direction of the frictional forces, we must first determine the direction in which the tension acts on each respective block. It is essential to understand that a rope always pulls an object - a rope can never push an object. Block 2 will be inclined to move to the left due to the presence of the force, F. Consequently, the tension in the upper portion of the rope will act to pull Block 2 in the opposite direction - to the right. We will therefore label the tension to be of magnitude T and in the right direction. In addition to this, the frictional force between Block 2 and Block 1 will act in the right direction to oppose the motion of Block 2 - I have labelled this frictional force as Fr2.

Turning our attention to Block 1, we can determine both the direction of the tension in the lower part of the cord as well as the direction of the frictional force between Block 1 and the floor. The cord is finite in length and will, in our model, not stretch (the pulley is frictionless and fixed, thus the tension in the rope must be constant and so the rope must not stretch for this to be the case). As a result, if Block 2 is to travel to the left, by definition, Block 1 must be pulled towards the pulley by the lower part of the cord. Consequently, the tension in the lower part of the rope, which will have the same magnitude, T, as the upper part, will act rightwards. To oppose this motion, the kinetic friction between Block 1 and the floor will act in the left direction - I will label this as Fr1.

Wow, that was a lot of analysis required for this question! With practice, however, you can work all of that out in your head within 20-30 seconds. We now have all the information that we need to construct a free-body force diagram. Using this diagram, we will be able to solve the question at hand. I have included my free-body force diagram below:

Our free-body force diagram.

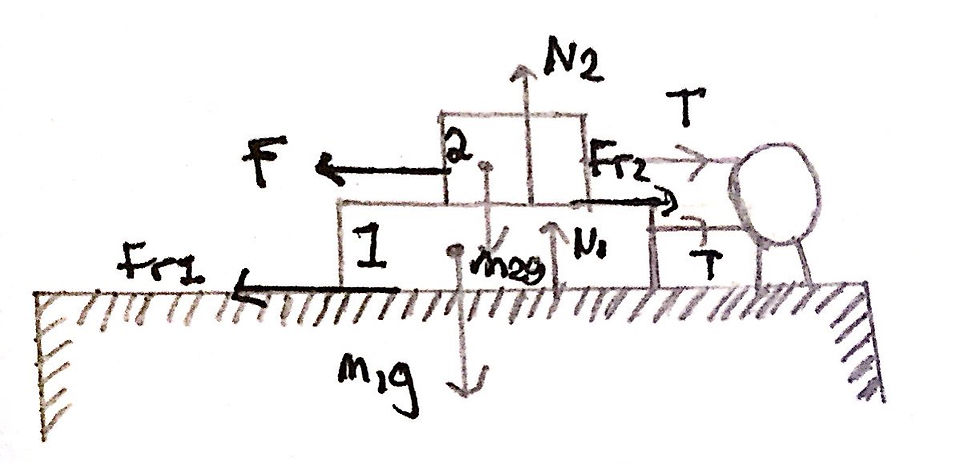
Finding the value of F:

In order for Block 2 to move to the left at a constant speed, the resultant force on Block 2 must be equal to zero. If Block 2 is to have zero acceleration (for it to be travelling at a constant speed), Block 1 must also be travelling at constant speed as the tension in the rope is constant and thus the acceleration of both objects is the same.

The maximum frictional force between two surfaces is equivalent to μN (where μ is the coefficient of kinetic friction and N is the normal reaction force between the two surfaces). Resolving upwards, we can determine that N2 is equal in magnitude to m2g and that N1 is equal in magnitude to m1g. Thus, the maximum frictional force between the surface of Block 2 and Block 1 is m2g*μ and the maximum frictional force between the surface of Block 1 and the floor is m1g*μ.

In order for the resultant force on Block 2 to be equal to zero, the external force, F, must be equal to the sum of the frictional force between Block 2 and Block 1 and the tension, T, in the upper part of the light cord. We also know, by considering Block 1, that the tension, T, in the lower part of the light cord is equal to the friction between Block 1 and the floor. As a result, we can set up two equations and eliminate the variable ‘T’ to create a final equation for the force, F. This is necessary as the variable T was never given to us in the question (unlike m1, m2 or μ) and so we must eliminate it from our final answer. I have included an image of my workings below:

Working out the final answer.

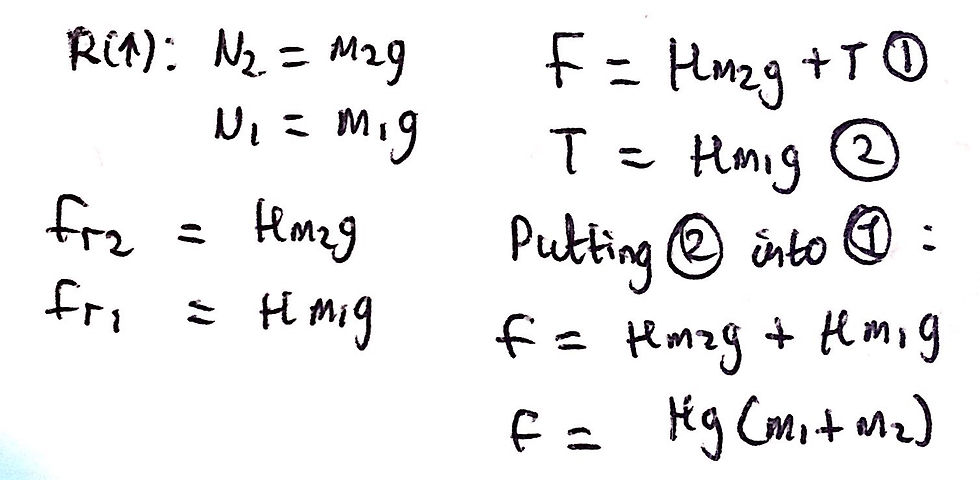
That is it for question four. If you have any questions about the problem, feel free to comment down below or email us on the Contact Us page. Stay tuned for solutions to be posted on the other questions!