MIT Problem Set 2 - Newton's Laws Question 5

Question 5: Blocks And Springs

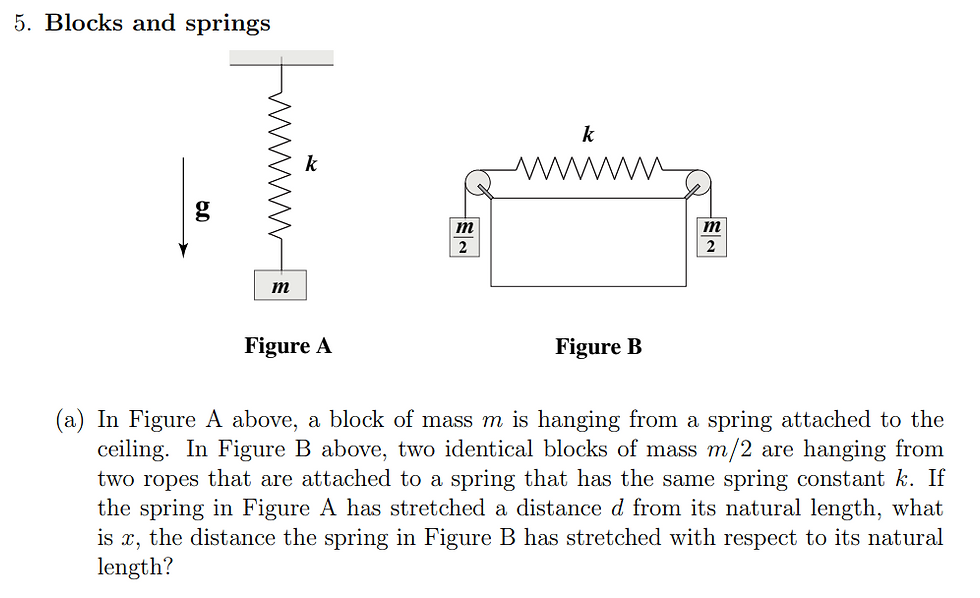
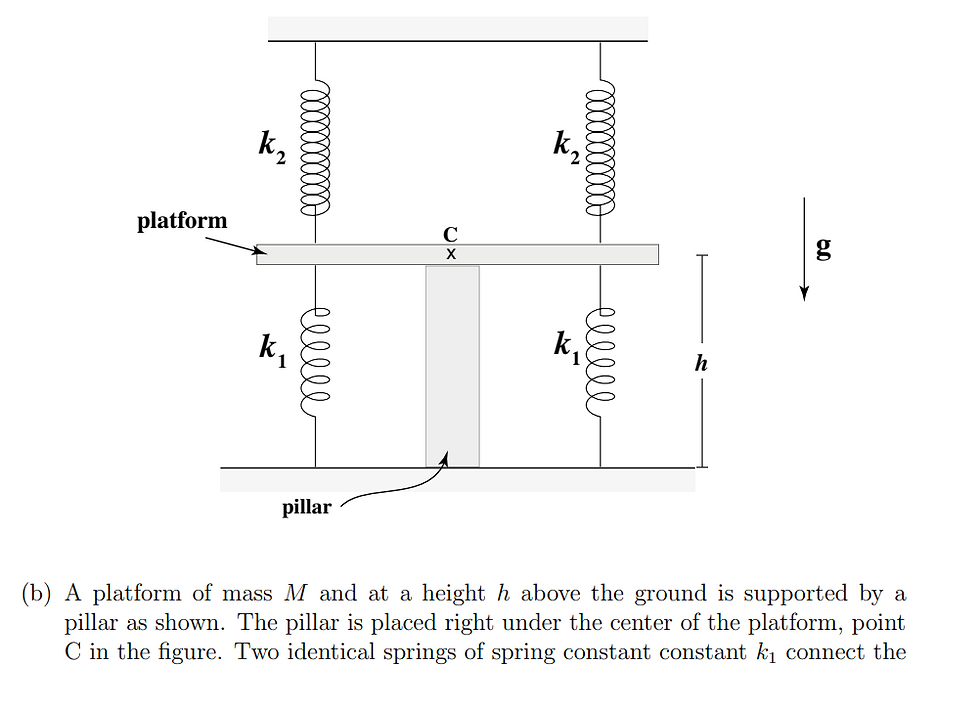
Image sourced: https://ocw.mit.edu/courses/physics/8-01sc-classical-mechanics-fall-2016/assignments/MIT8_01F16_pset2.pdf

Theoretical Analysis:

Part a:

In the first part of the question, we have two different spring configurations. When you see springs, you should immediately think of Hooke’s law. The law states that the extension of a spring is directly proportional to the force that is applied to it provided the limit of proportionality is not reached - this is often mathematically summarised as F=kx, where k is the spring constant or the constant of proportionality.

Looking at Figure A, it should be clear that there are two forces acting on the spring. The weight of the block, mg, acts vertically downwards and, in return, causes a tension in the spring to act vertically upwards in the opposite direction. This tension will have the same magnitude as the weight of the block - mg. Since this force causes the tension in the spring, we can equate mg and kx. We are given that the extension of the spring is d in the question, as this is the distance that the spring has stretched from its natural length, and so we can substitute this in for x. From here, we can rearrange for d as I have done so in the image below:

Working out the extension for the spring in Figure A.

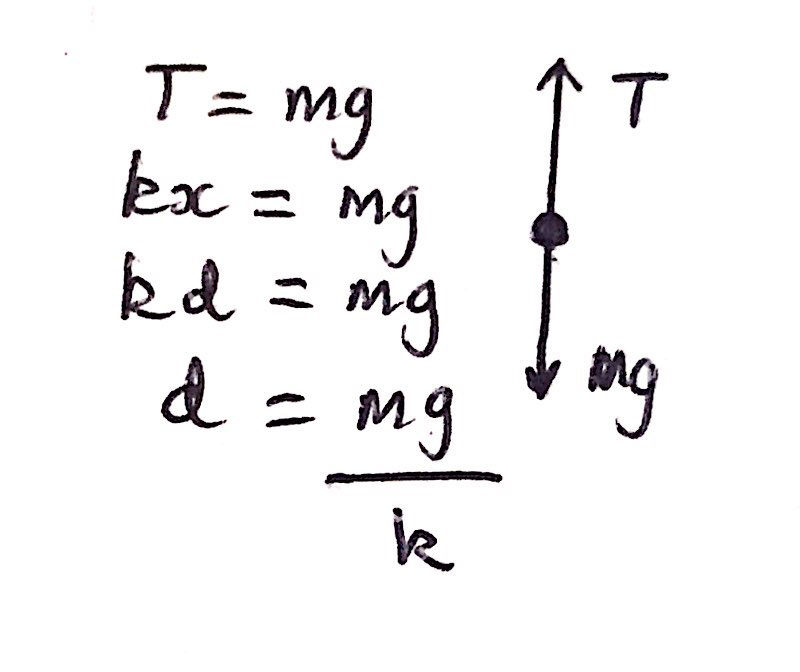
Now that we have an expression for d, we can find an equivalent expression for the extension of the spring system in Figure 2. This will thus allow us to compare the extensions in the two spring systems and to therefore find the value of x, the extension of the spring system in Figure B, in terms of d, the extension of the spring system in Figure A.

Looking at Figure B, we can see two blocks with mass m/2. Therefore, their weights should be acting vertically downwards respectively with magnitude mg/2. This, as a result, causes there to be a tension in the spring, resulting in the spring extending by a value of x. The key to answering this question is to think conceptually about what is really going on. We can take the centre of mass of the spring system to be fixed by symmetry and thus we only need to consider one half of the spring. In effect, the tension in the spring will be due to a block of mass m/2. Therefore, the tension in the spring will have a magnitude of mg/2. From here, we can set mg/2 to be our force in the equation F = kx. Now, we can rearrange for x and deduce our final answer from our expression for the spring system in Figure A. I have included my workings and answer below:

Calculating the value of x in terms of d.

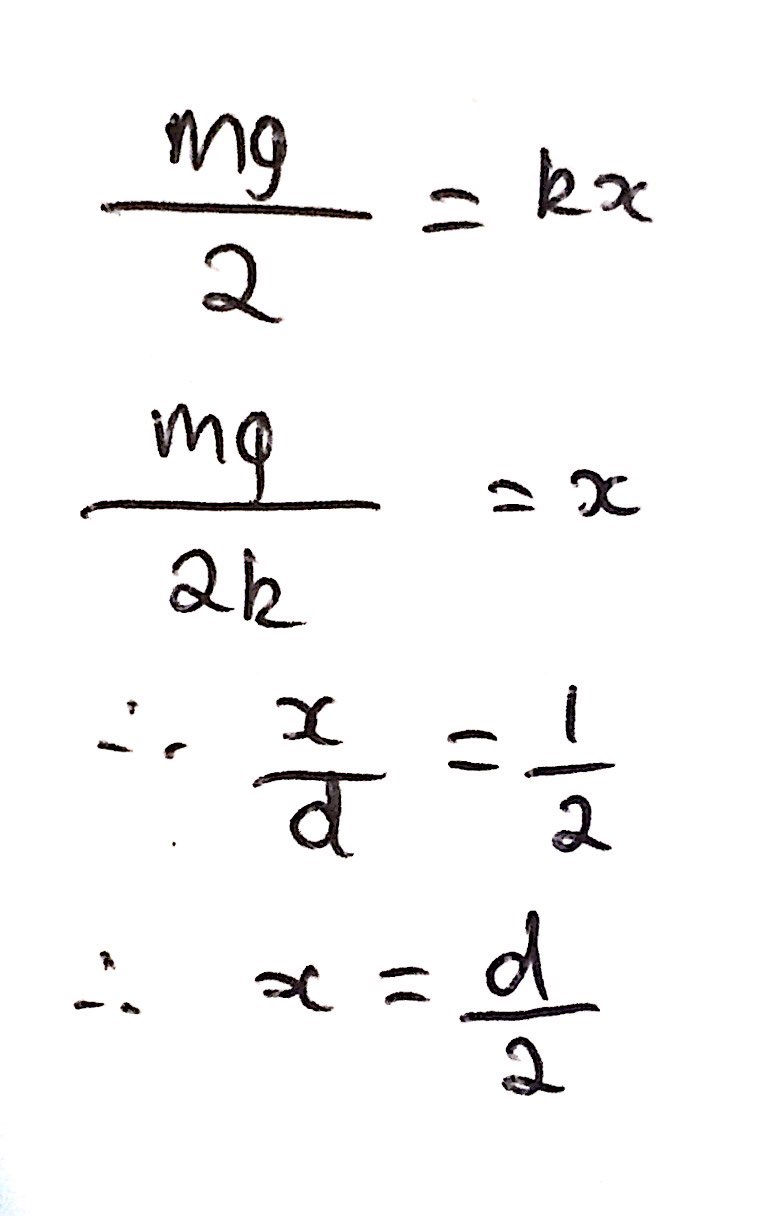
That is Part A complete; now we can move onto Part B!

Part B:

This part of the question seems very difficult and different to the majority of the high school Physics questions that involve springs and Hooke's law. But, the key to this problem is to simplify the problem as much as possible. In fact, we can use a very neat, little trick from the very beginning. There are two identical springs above the platform and below, as given in the question. However, we can 'create' two springs that are equivalent to the two upper springs as well as the two lower springs, respectively. To do this, we just need to know that the effective spring constant (so the equivalent spring constant that one spring would have) for two (or more) parallel springs is just the sum of each spring constant (i.e. k1 + k2). If you are like me and you want actual mathematical proof of this rather than just trusting someone else's word for it, then please refer to the image below where I prove this fact:

Proving that you can add spring constants in a parallel arrangement.

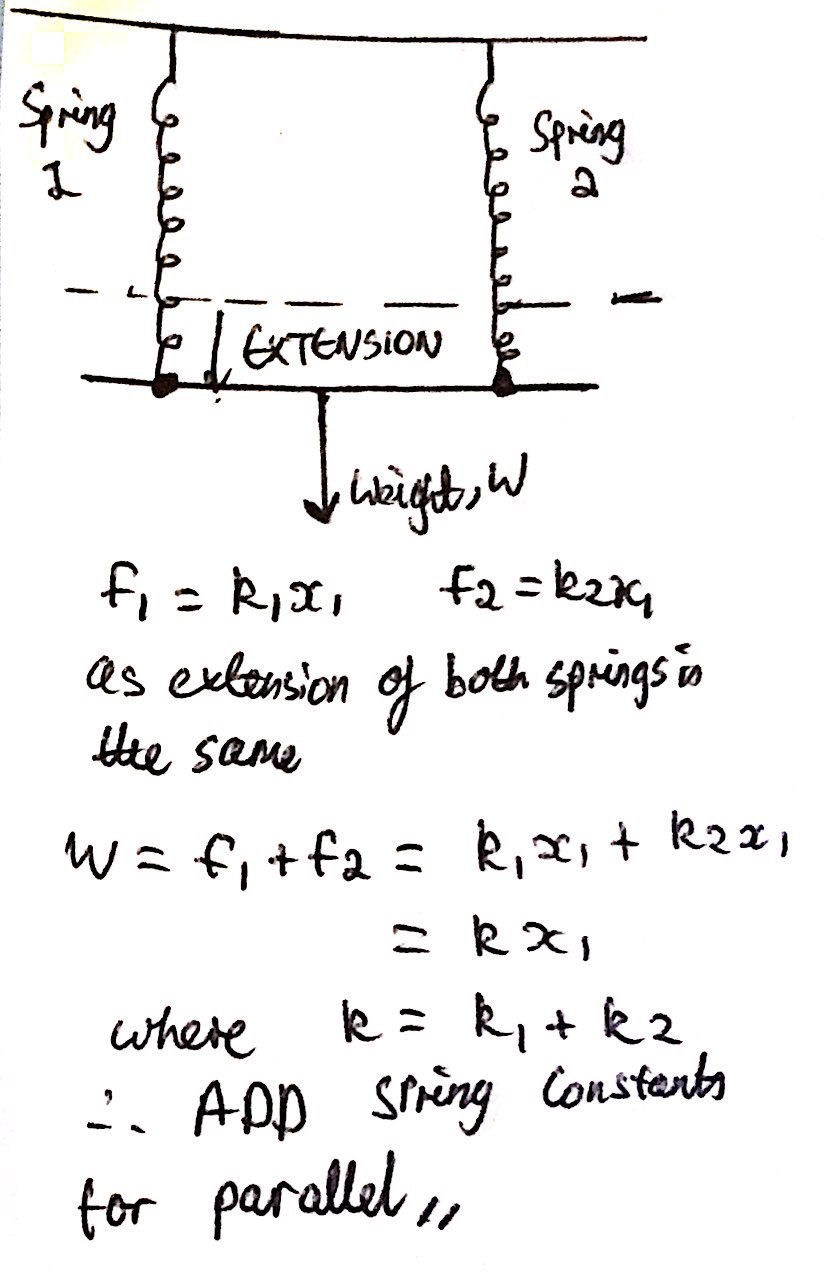
Consequently, we can now replace the two upper springs with one spring that has a spring constant of 2k2, and, likewise, we can replace the two lower springs with one spring that has a spring constant of 2k1. Thus, we have already simplified our problem and we haven't had to do any complicated maths.

We don't actually have to worry about forces for the time being. When the pillar is supporting the platform, the springs are unstretched. This means that the springs are in equilibrium and share the same equilibrium point - this will prove very useful for later.

Now, when the pillar is removed, the springs will stretch as a result of the weight of the platform. The upper spring will extend; I shall label this extension as x1, and, as a result of this, the lower spring will compress by x2. The important thing to note is that springs will always pull or push towards their natural equibilirium position. Therefore, if the platform's weight, Mg, is acting vertically downwards, the tensions in both springs will be acting upwards to restore each spring to its natural equilibrium position. Remember, like we discovered before, both springs have the same equilibrium position and therefore the tensions will act in the same direction as to restore each spring to its equilibrium position.

From Hooke's law, the tensions in each respective spring have the magnitude of 2k2x2 and 2k1x1, which we can then set equal to the weight of the platform Mg. This creates our first equation. Subsequently, we can create our second equation by recognising that the compression of the lower spring, x1, must be equal to the extension of the upper spring, x2. We will call the generic extension of both springs, x. This should be intuitively clear and is supported by the fact that both springs were not extending when the pillar was in place - both springs have the same equilbrium position. From here we can write down the two equations that we need. I have also included a free-body force diagram of what is currently going on below:

Free-body force diagram of the problem.

The two equations that we need.

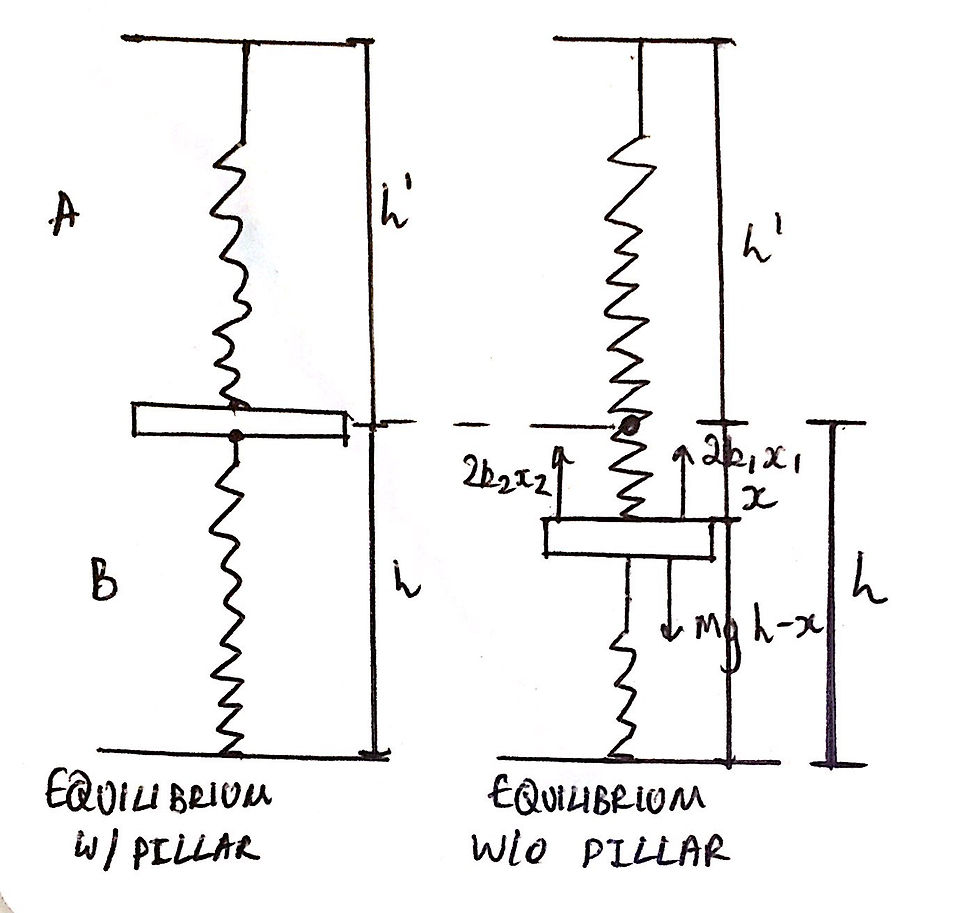
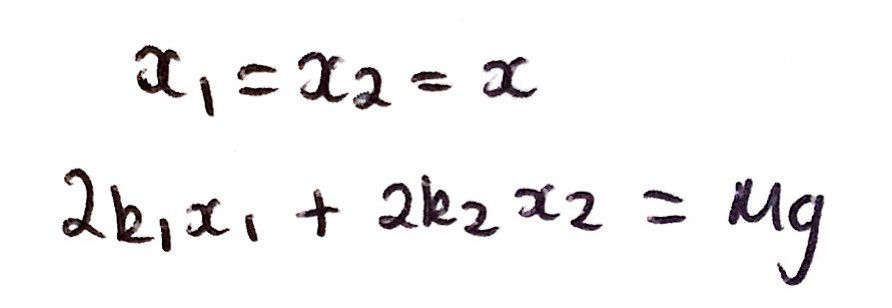
From here, the maths is quite simple if you can recognise one neat little trick. Since the extension of both springs is the same, we can just factor out x and rearrange the equation to solve for x. Now, we must be very clear at what x really means. If the upper spring extends by x, the platform must decrease in height by a distance of x. In turn, the lower spring will automatically be compressed by the same distance x. Therefore, the value of h will decrease by the same amount, x. Thus, to answer the question, we just have to state that the new height will just be the initial height, h, minus the extension of the springs, x. We cannot use x in our final answer as we are only allowed to express our answer in terms of h, M, g, k1, and k2. However, we already have an expression for x and thus we can just sub in our expression for x as it only contains 'allowed' variables. Thus, our final answer is as shown in the image below:

Final answer to Part B.

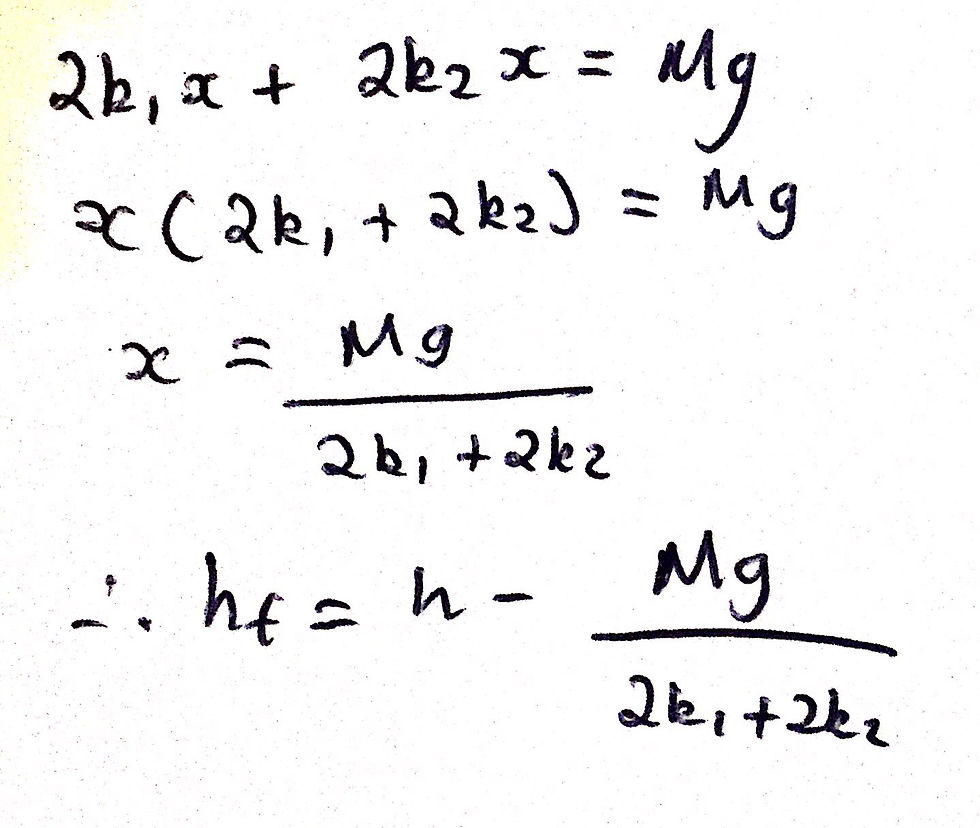
That is it for question five. If you have any questions about the problem, feel free to comment down below or email us on the Contact Us page. That is also the end of the solutions for Problem Set 2. I have very much enjoyed solving these problems and sharing my solutions with you all. If you would like me to solve any other problem sets, please comment down below. Thank you!