What is this?
Massachusetts Institute of Technology (MIT) have released courses, which are available to the public, along with some assignments. These are all aimed at the undergraduate level. The assignments can be found here: https://ocw.mit.edu/courses/physics/8-01sc-classical-mechanics-fall-2016/assignments/ I decided to complete Problem Set 3 as I wanted to challenge myself with harder circular motion questions. I realised that there was no official/unofficial mark scheme and thus decided to post my workings.
Note: I do not recommend simply copying down these answers but rather I strongly suggest for you to tackle these problems as long as possible and use my workings as a last resort - I cannot guarantee that they are correct as I completed them independently. I will be uploading solutions to each question separately, with this post introducing the subsequent posts as well as tackling the first question.
Question 1: Bead on a Rotating Hoop
Image sourced: https://ocw.mit.edu/courses/physics/8-01sc-classical-mechanics-fall-2016/assignments/MIT8_01F16_pset3.pdf
Theoretical analysis:
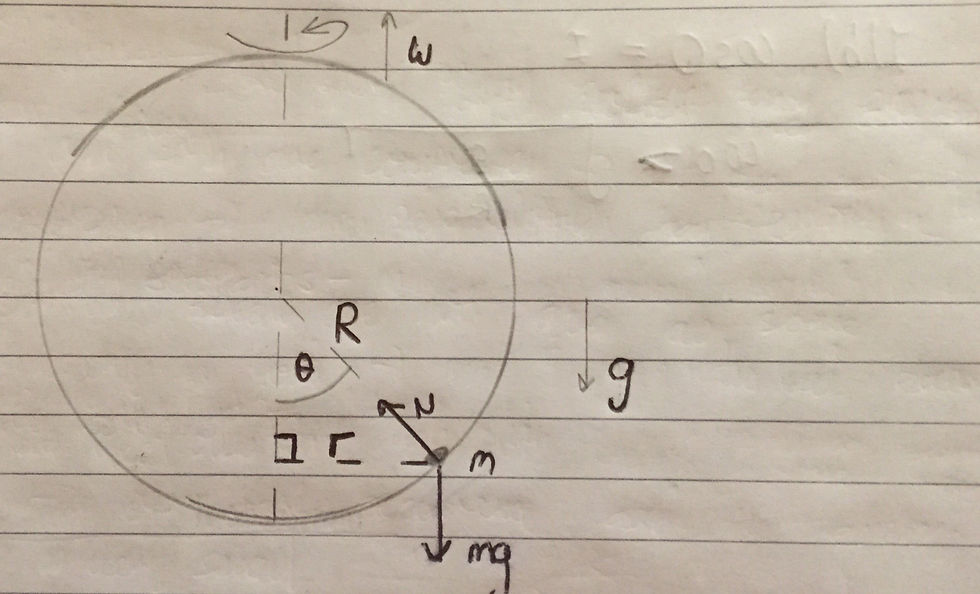
Initially this question can seem very confusing however it is important to break it down. The hoop is rotating anticlockwise relative to the axis of rotation (denoted by the dotted line) as shown in the diagram. It is important to notice that the radius R is not the radius, which I shall denote as r, of the bead’s circular motion. As can be seen in my drawing above, there is a normal contact force, N, which acts perpendicular to the bead’s point of contact with the hoop. Moreover, the weight, mg, of the bead acts straight down (parallel to the direction of gravity as shown).
Part A:
The first step in a problem like this is to consider what is providing the centripetal force, which acts towards the axis of rotation. There are only two forces acting on the bead (the loop is frictionless). The weight has no horizontal component and thus does not affect the centripetal force. Resolving in the horizontal direction, it should therefore be apparent that the centripetal force is provided by Nsinθ. Resolving in the vertical direction we can state that Ncosθ=mg. You should recall that the centripetal force is equal to m*ω^2*r. However, as aforementioned, we are not permitted to use r in our answer and thus we must express r in terms of R. Using trigonometry, it is apparent that Rsinθ = r.
We now have two equations:
Ncosθ = mg (1)
Nsinθ = m*ω^2*Rsinθ (2)
Now that the theoretical understanding is in place, the rest is simple algebraic manipulation. An important trigonometric identity that will appear a lot in circular motion is that sinθ/cosθ = tanθ, which I have used implicitly in my calculations below.
Part B:
This part of the question is simply a follow-up to see whether you truly understand the equation you have just derived. If the angle θ has to be equal to 0 for the bead to be in a balanced position, then cosθ must ultimately be equal to 1 (as cos 0 = 1). Thus the following statement can be made:
That is it for question one. If you have any questions about the problem, feel free to email us on the Contact Us page. Stay tuned for solutions to be posted on the other questions.
コメント