Question 2: Banked Turn
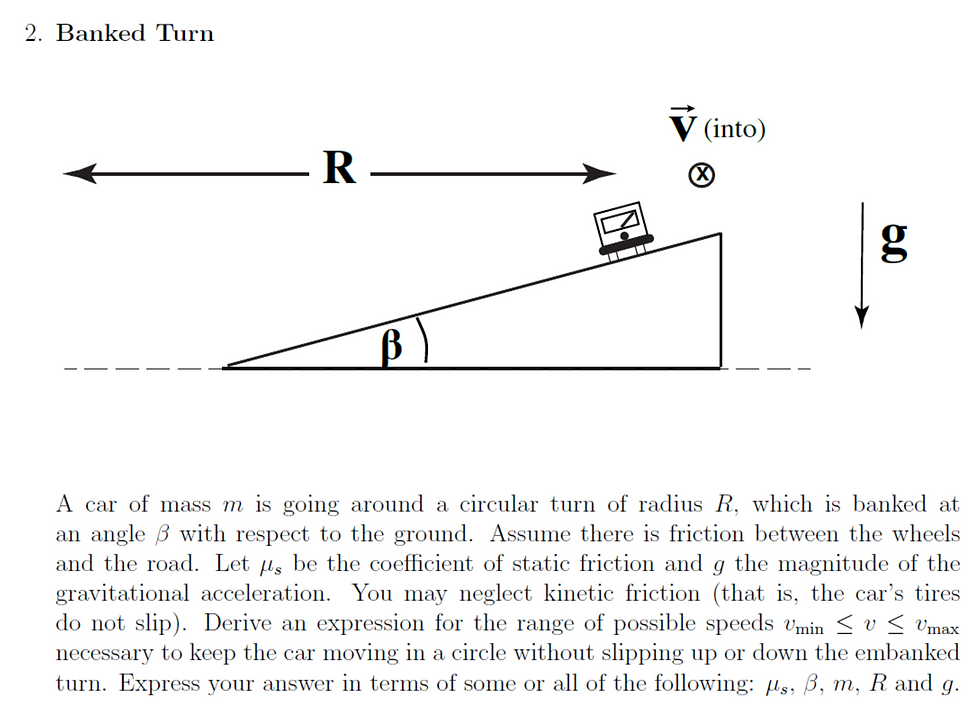
Image sourced: https://ocw.mit.edu/courses/physics/8-01sc-classical-mechanics-fall-2016/assignments/MIT8_01F16_pset3.pdf
Theoretical analysis:
This problem involves a car going around a banked turn - similar to a cyclist in a velodrome. A centripetal force is required to turn the car. At a specific speed, which I will call Veq, the centripetal force required to turn the car is exactly equal to the horizontal component of the normal reaction force between the car and the road, labelled as N. At speeds above and below Veq, a frictional force, denoted as F, will be required to keep the car in its circular motion. You should recall that the maximum force of static friction is equal to μN, where μ is the coefficient of static friction between two surfaces - in this case the wheels and the road. Therefore, eventually the speed of the car, v, will be such that the frictional force will no longer be large enough to prevent the car from slipping up or down the slope - these are the respective velocities we have to find. I will consider each respective case separately so that we can calculate Vmin as well as Vmax.
V > Veq:
If the speed of the car is greater than Veq, the horizontal component of the normal reaction force, which is Nsinβ, will not be large enough to keep the car in circular motion and thus the car will 'attempt' to slip up the road. The frictional force, F, will oppose this motion. As with any question, it is important to begin by drawing a free body diagram as I have included above. The weight of the car, mg, will act straight down, parallel to the direction of gravity as shown in the diagram. The normal reaction force, N, will act perpendicular to the car's point of contact with the road. In this case, the frictional force, F, will act down the slope and parallel to it. The radius of the car's circular motion is given as R.
If we resolve in the vertical direction, we can state that Ncosβ = mg + Fsinβ (1). The centripetal force is provided by the horizontal component of the normal reaction force as well as the horizontal component of the frictional force. We can therefore say that Nsinβ + Fcosβ = (m*v^2)/R (2). All we need to do now is use the fact that F = μN (as we are considering the case when friction is at its maximum) and rearrange equation (1) for N and substitute this into equation (2). The rest is just algebraic manipulation as we have to rearrange for v. We will therefore obtain the maximum speed (Vmax) at which any larger speeds will result in the car slipping up the slope. I have included my calculations below:
V < Veq:
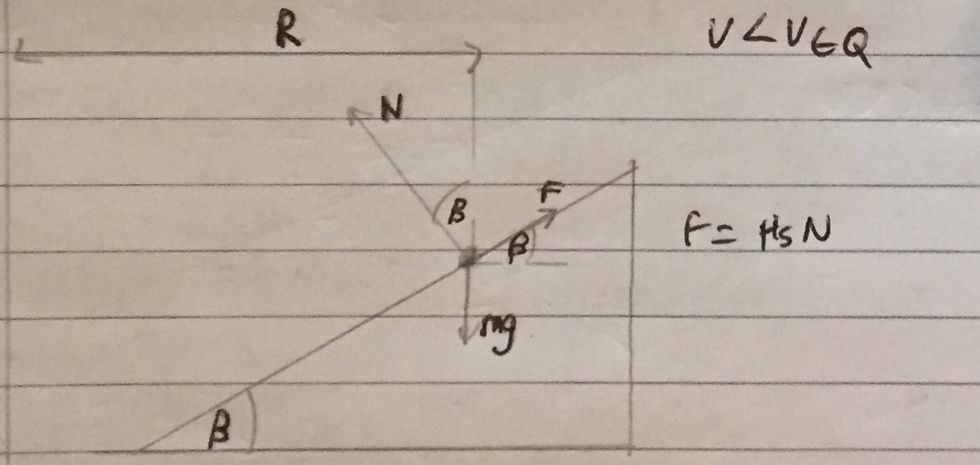
This case is very similar to the one we just solved however we are considering what happens when the speed of the car is below Veq. It should be apparent that the frictional force will act in the opposite direction as before as the car will 'attempt' to slip down the road. The free body diagram (shown above) is therefore very similar. Resolving forces vertically we can state that mg = Ncosβ + Fsinβ (1). The centripetal force will be provided by the horizontal component of the normal reaction force minus the horizontal component of the frictional force, which is acting in the opposite direction. In other words, Nsinβ - Fcosβ = (m*v^2)/R. As before, we use the fact that F=μN to rearrange equation (1) for N. We can then substitute this into equation (2) and solve for v, giving Vmin. I have included the respective calculations below:
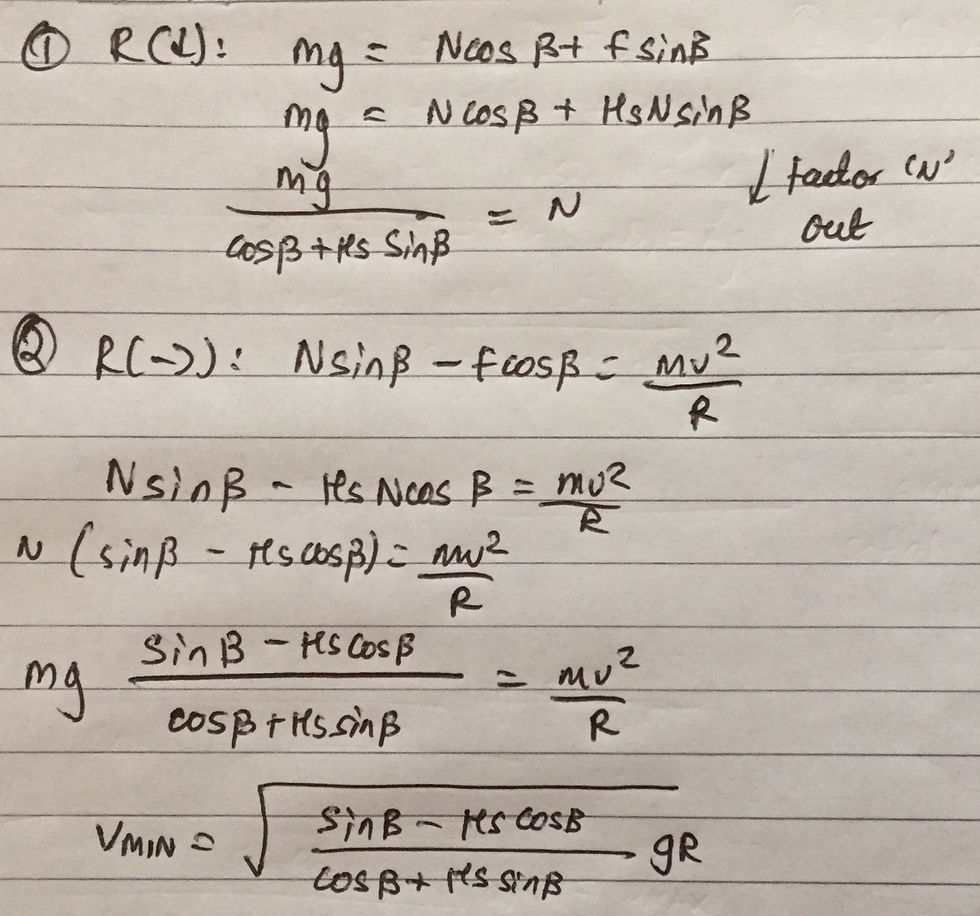
Tying this all together we can conclude by stating the answer as:
That is it for question two. If you have any questions about the problem, feel free to email us on the Contact Us page. Stay tuned for solutions to be posted on the other questions.
Comments