Question 3: Tetherball Breaking Off
Image sourced: https://ocw.mit.edu/courses/physics/8-01sc-classical-mechanics-fall-2016/assignments/MIT8_01F16_pset3.pdf
Theoretical analysis:
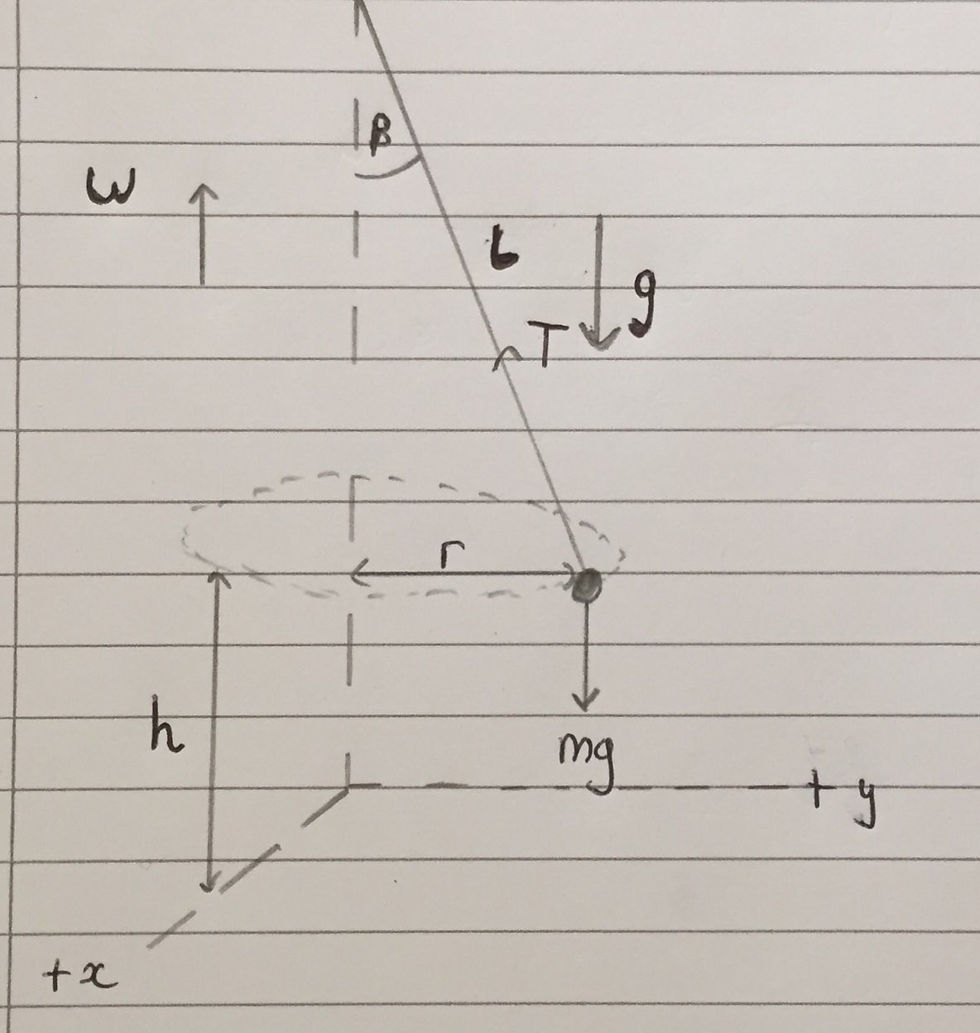
This problem involves a ball that is revolving in a circle, which is suspended by a string. Therefore, there must be tension in the string, which I will denote as T. I am assuming that the string is light. In other words, the string is assumed to have negligible/no mass and thus the tension is the same throughout the length of the string, and the mass of the string can be ignored when treating the system as a whole. The weight of the ball, which I have labelled as mg, acts straight down as shown in the free body diagram included above. The string is of length L and I have labelled the radius of the ball's circular motion as r.
Part A:
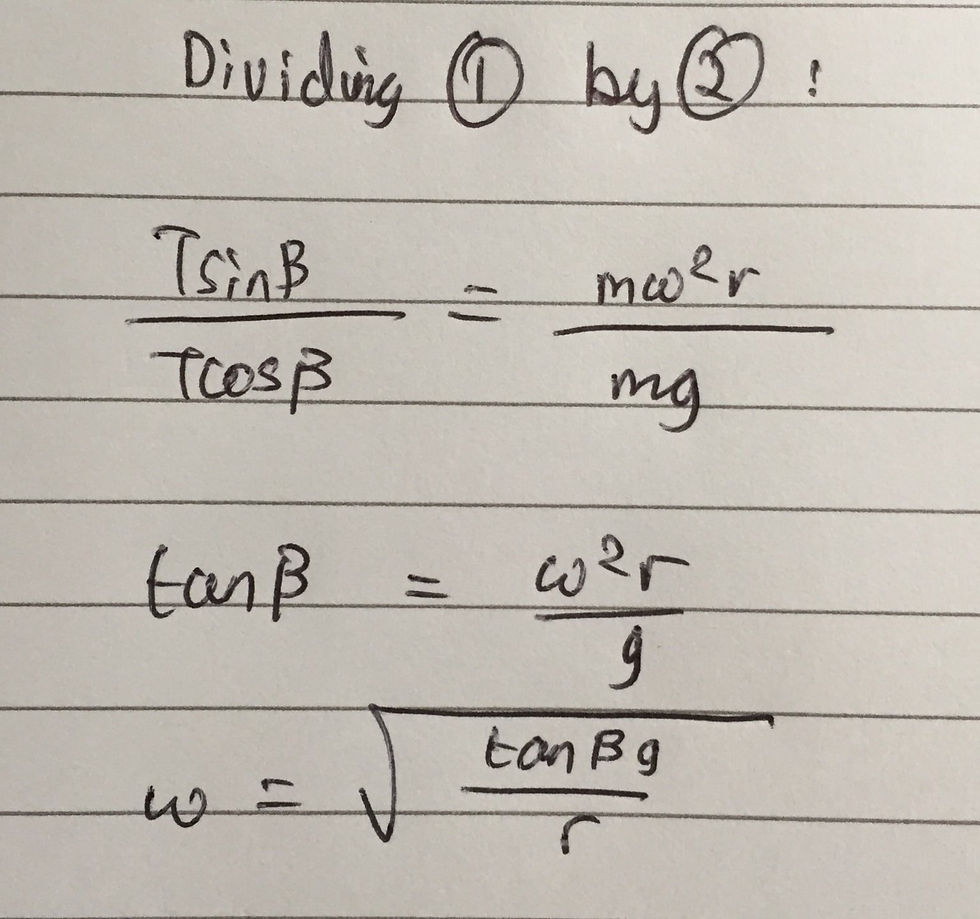
The only force acting upon the ball that has a horizontal component is the tension, T, in the string. Therefore this must provide the centripetal force. We can thus state that Tsinβ = m*ω^2*r (1). Furthermore, if we resolve vertically, we can state that mg = Tcosβ (2). Now, you can divide equation (1) by equation (2) and rearrange for ω. I have included my calculations below:
This however is not the final answer to part A as we are not permitted to use r within our answer. But, from trigonometry, it should be apparent that Lsinβ = r. We can therefore use this fact, as well as that tanβ = sinβ/cosβ, to reach a simplified answer as I have included below:
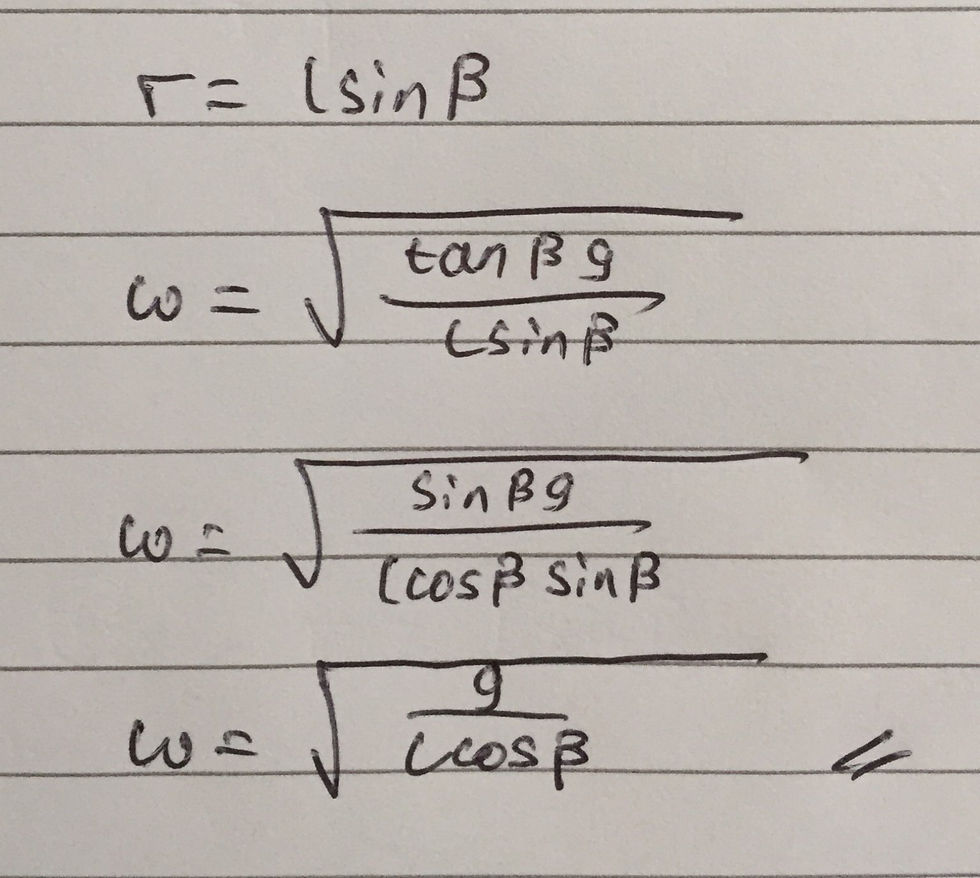
Part B:
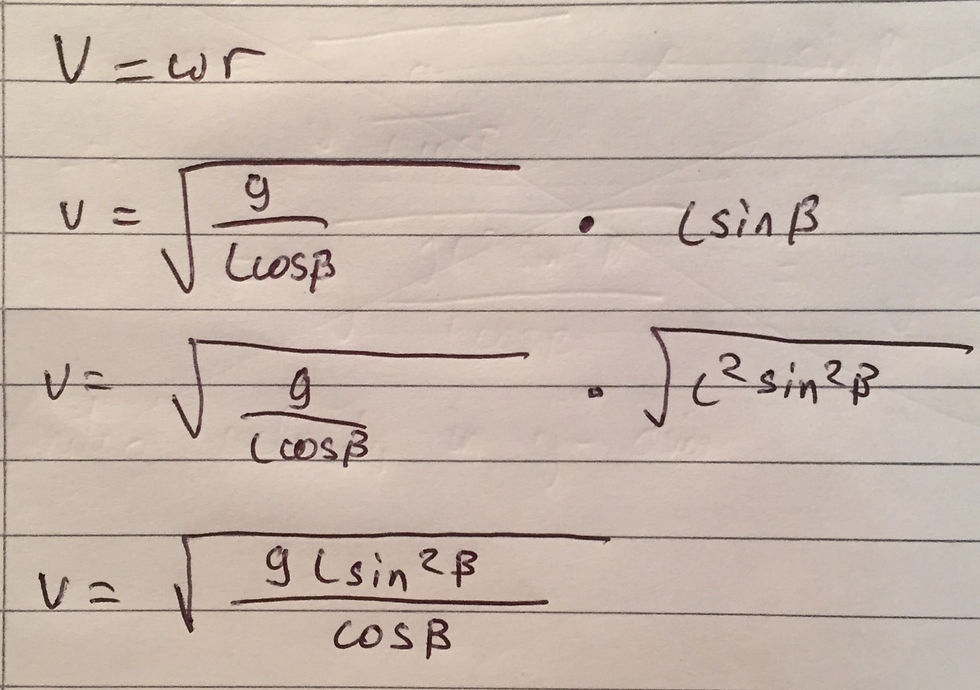
This part of the question is essentially testing whether you can apply the (SUVAT) equations of motion in an unfamiliar context. We can model the ball as a projectile and thus motion in the horizontal and vertical directions can be considered independently. Moreover, the question allows us to assume that there is no air resistance. The first step is to convert the angular velocity of the ball into the translational equivalent. This can be done using the equation v = ωr. We must, however, substitute in the fact that Lsinβ = r as the use of r is not permitted in the final answer. The translational velocity of the ball can then be calculated as follows:
Now that we have the translational velocity, v, in terms of the permitted variables, we can apply the equations of motion in order to calculate the horizontal distance, d, that the ball traverses before hitting the ground. Firstly, we must consider the motion in the vertical direction. We can use the equation s = u*t + 0.5*a*t^2 in order to calculate the time that the ball takes to fall and collide with the ground.
The initial vertical velocity of the ball is zero as the resultant force acting on the ball acts only in the horizontal direction (the resultant force is the centripetal force in this case). The ball will fall a vertical distance of h. Also, we can consider the ball to be in free fall as, while it is falling, it will be under the influence of gravity alone and thus the acceleration of the ball will be equal to g. The final velocity of the ball is irrelevant to this question. We can thus input all the relevant variables into the equation and find the time taken, t, in terms of h and g. I have included my calculations below:
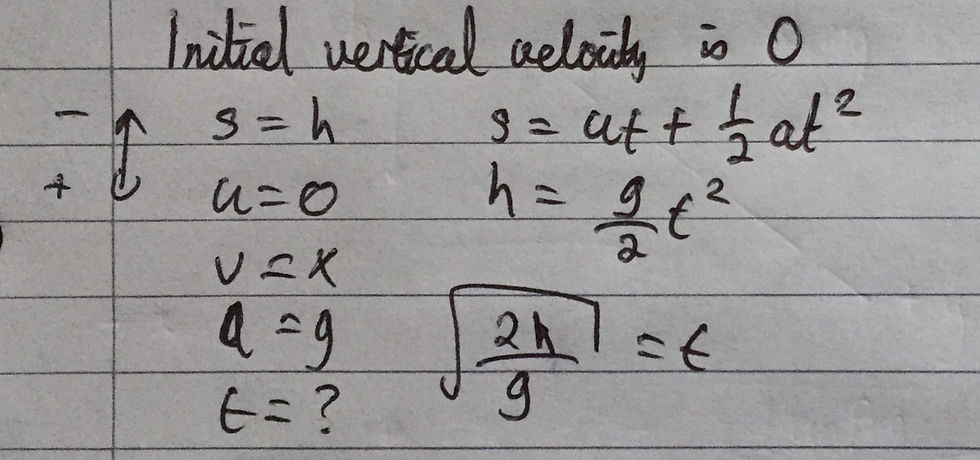
We can now consider motion in the horizontal direction. As acceleration in the horizontal direction is zero (the acceleration of the ball due to gravity has no horizontal component), we can calculate the distance, d, by multiplying the translational velocity, v, by the time taken, t, which we calculated previously. The final answer is as follows:
That is it for question three. If you have any questions about the problem, feel free to email us on the Contact Us page. Stay tuned for solutions to be posted on the other questions.
Comments