MIT Problem Set 3 - Circular Motion Question 4

Question 4: Two Boxes Around a Shaft

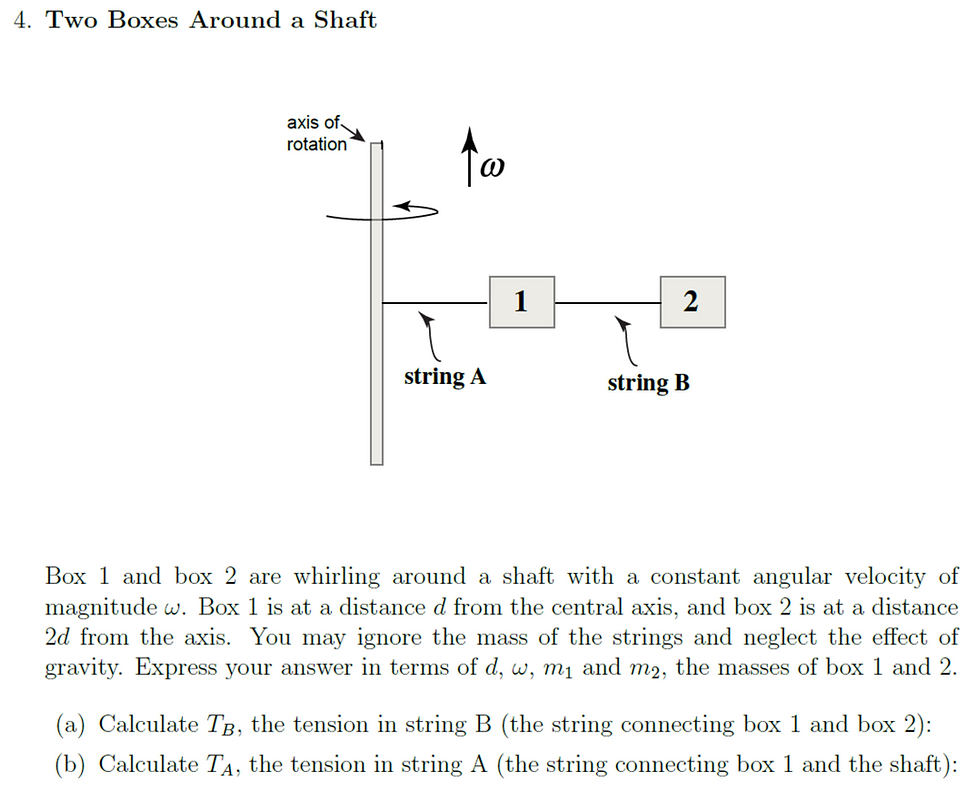
Image sourced: https://ocw.mit.edu/courses/physics/8-01sc-classical-mechanics-fall-2016/assignments/MIT8_01F16_pset3.pdf

Theoretical analysis:

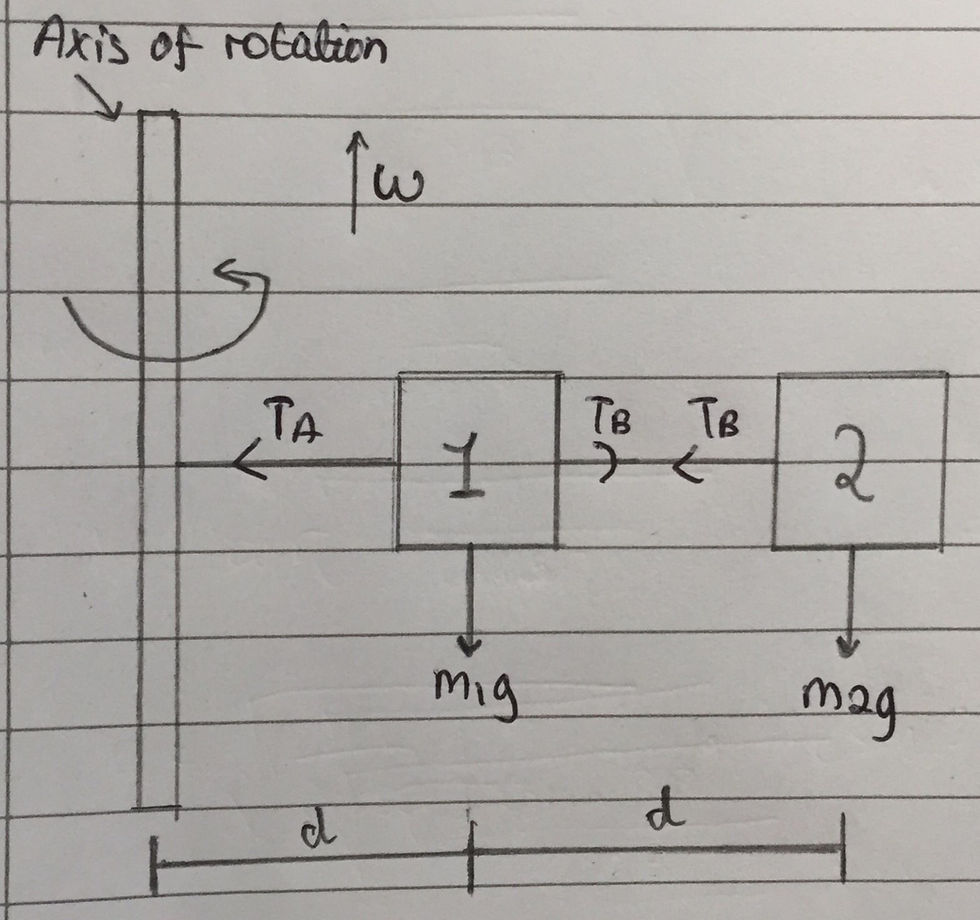
In this problem we have two boxes, of different masses, which are rotating around a shaft with the same angular velocity, ω. Box 1 is at a distance d from the axis of rotation and Box 2 is at a distance 2d from the axis. The tension in string A is labelled in my diagram as Ta. The tension in string B is labelled as Tb. The important thing to remember about tension in a string is that it cannot push an object but rather it must pull the object. Therefore, the tension, Tb, acts on Box 1 in an opposite direction to the direction in which it acts on Box 2. I have also labelled the weight of each respective box, however the question allows us to neglect the effect of gravity. I have included the free body diagram above.

Part A:

We can analyse each box independently. For this part of the question, we must focus primarily on Box 2, in order to find the tension, Tb, in string B. The only horizontal force acting on Box 2 is the tension in string B. The radius of the box's circular motion is 2d. Therefore, we can state that Tb = m*ω^2*2d, where m is the mass of Box 2, giving us the answer for part A.

Part B:

Using our answer for Part A, we can now find the tension, Ta, in string A by focusing on Box 1. The centripetal force on Box 1 is provided by the tension in string A, Ta, minus the tension in string B, Tb, as Tb acts in the opposite direction to Ta. The radius of the box's circular motion is d. This gives us the equation: Ta - Tb = m*ω^2*d, where m is the mass of Box 1. We can then substitute in the equation we already have for Tb and rearrange the equation for Ta in terms of the permitted variables, giving the final answer. I have included my workings for part A and part B below:

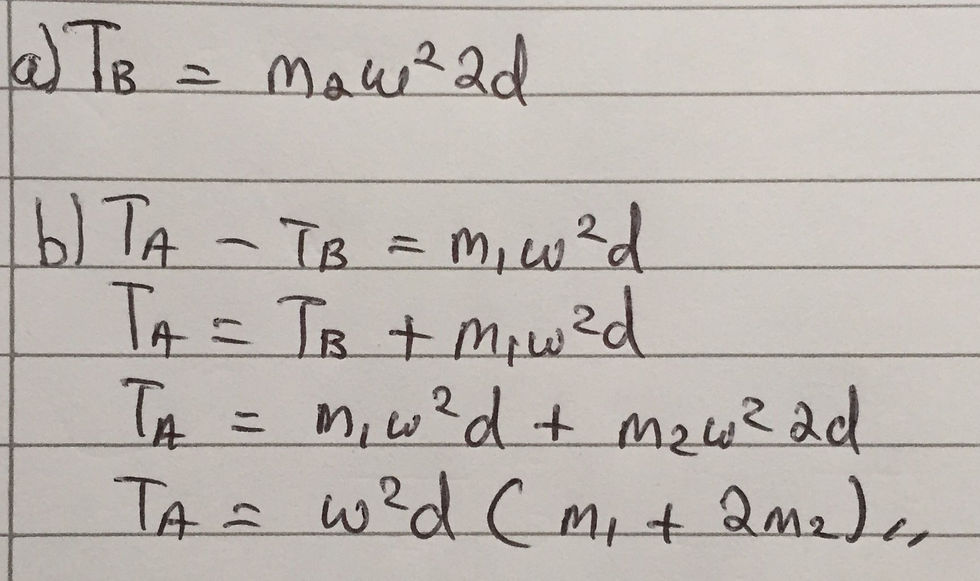
That is it for question four. If you have any questions about the problem, feel free to email us on the Contact Us page. Stay tuned for solutions to be posted on the other questions.