Question 5: Satellite
Image sourced: https://ocw.mit.edu/courses/physics/8-01sc-classical-mechanics-fall-2016/assignments/MIT8_01F16_pset3.pdf
Theoretical analysis:
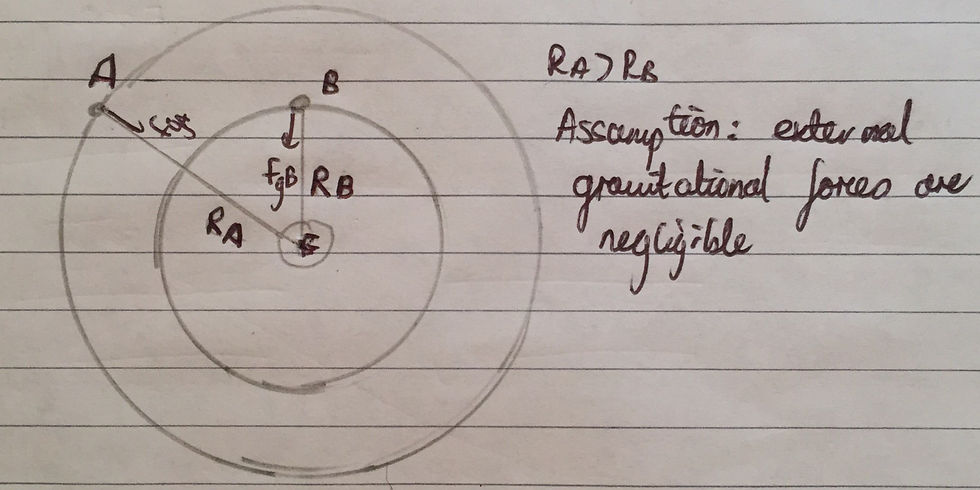
There are two satellites of equal mass, m, which are orbiting around the earth at different altitudes. We are allowed to assume that the orbits are circular. I have also made the assumption that any external gravitational forces (other than the gravitational force of attraction between the Earth and each respective satellite) are negligible. Moreover, I have assumed that the radius of the orbit of satellite A, which I have labelled as Ra, is greater than the radius of satellite B's orbit, denoted as Rb. The Earth and each respective satellite exert a gravitational force of attraction on each other. For each satellite, this force is directed towards the centre of the Earth. I have labelled each force as Fga and Fgb respectively. I have included a free body diagram above.
Part A:
If we focus on satellite A, it should be apparent that the centripetal force is equal to the gravitational force of attraction between the Earth and the satellite. According to Newton's law of universal gravitation, this force is equal to (GMm)/R^2. G is the universal gravitational constant (equal to approximately 6.67*10^-11 Nm^2/kg^2), M is the mass of the Earth (in this case) and m is the mass of the satellite (M and m simply refer to the mass of the two bodies in question). R refers to the distance between the two masses, which are satellite A and the Earth in this case. We do not actually need to know the value of any of these variables as we are simply comparing the translational speeds of each satellite. Using this we can state that (mv^2)/R = (GMm)/R^2. We now just have to rearrange the equation for v, as I have done so below (Ma refers to the mass of satellite A and Me refers to the mass of the Earth):
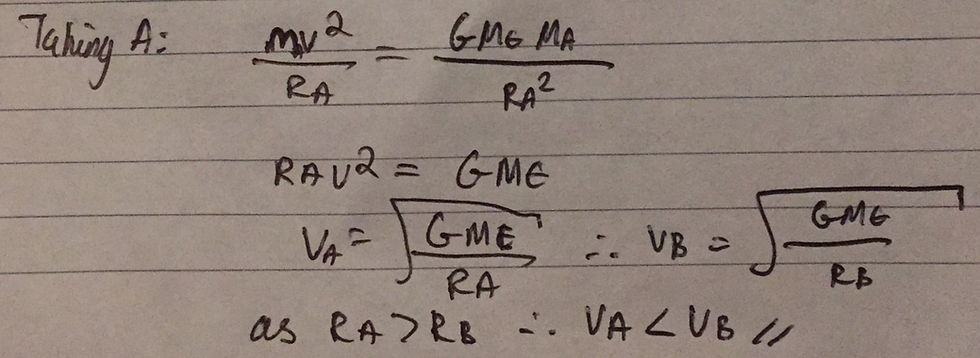
The result for satellite B will yield a similar value to the speed of satellite A, Va, but instead of the denominator being Ra it will be Rb. Therefore, as we assumed that Ra is greater than Rb and the numerator (GMe) is common to both Va and Vb, Va must be less than Vb. In other words, satellite B will orbit at a higher speed around the Earth than satellite A.
Part B:
In order to answer this part of the question, we will derive Kepler's Third Law; which states that for planets (but it applies to satellites as well) in circular orbits, the square of the time period, T, is proportional to the cube of the radius of the orbit, R - in other words, T^2 = kR^3, where k is simply a constant of proportionality. We will again use the concept that the centripetal force on satellite A is equal to the gravitational force of attraction between the satellite and the Earth. However, this time we will state that m*ω^2*R = (GMm)/R^2. We can rearrange this equation to obtain ω^2*R^3 = GM (1) (where M is the mass of the Earth). You should recall that ω = 2π/T (2), where T is the time period of the body in circular motion (the time period is the time taken for the object to make one complete orbit). Substituting equation (2) into equation (1) gives us (4*π^2*R^3)/T^2 = GM. This is essentially a rearranged version of Kepler's Third Law, where k is equal to 4π^2/GM. Subsequently, we just have to rearrange the equation for T, as I have done so below (Ta refers to the time period of satellite A and ωa refers to its angular velocity):
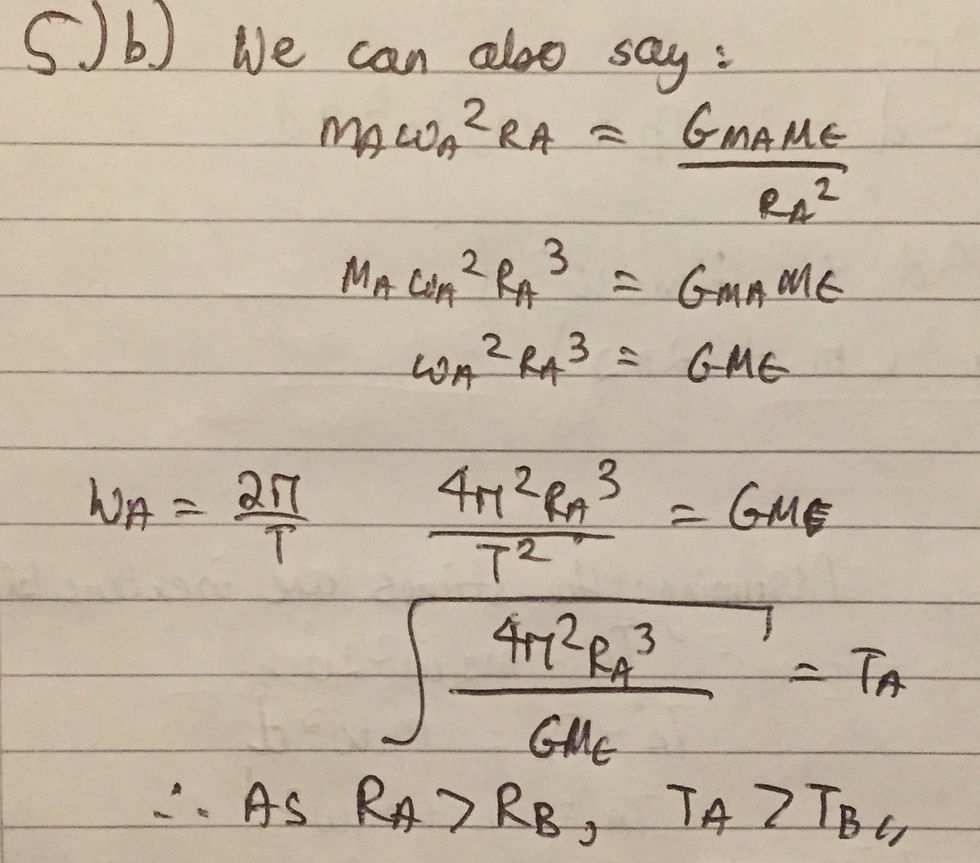
Completing the same process for satellite B will yield a similar answer with Rb in the numerator instead of Ra. The denominator GMe is common to both Ta and Tb. Thus, as Ra is greater than Rb the time period of satellite A will be greater than the time period of satellite B. Of course, one could have come to the same conclusion without considering circular motion equations per se. The velocity of satellite A (as analysed in part A) is smaller than the velocity of satellite B and the radius of its orbit Ra is greater than the radius of satellite B's orbit, Rb. Consequently, as the orbits are assumed to be circular, satellite A will travel a greater distance (Ra*2π - the circumference of the circle) and since it is travelling at a smaller speed, it must take a longer time to complete one orbit, resulting in a larger value for its time period. However, I prefer the previous method as it is independent of any calculations we made in part A, as well as the fact that it derives Kepler's Third Law, which is extremely useful to know when considering the circular motion of planets.
That is it for question five. If you have any questions about the problem, feel free to email us on the Contact Us page. Stay tuned for solutions to be posted on the other questions.
Comments