MIT Problem Set 3 - Circular Motion Question 6

Question 6: A coin on a rotating disk

Image sourced: https://ocw.mit.edu/courses/physics/8-01sc-classical-mechanics-fall-2016/assignments/MIT8_01F16_pset3.pdf

Theoretical analysis:

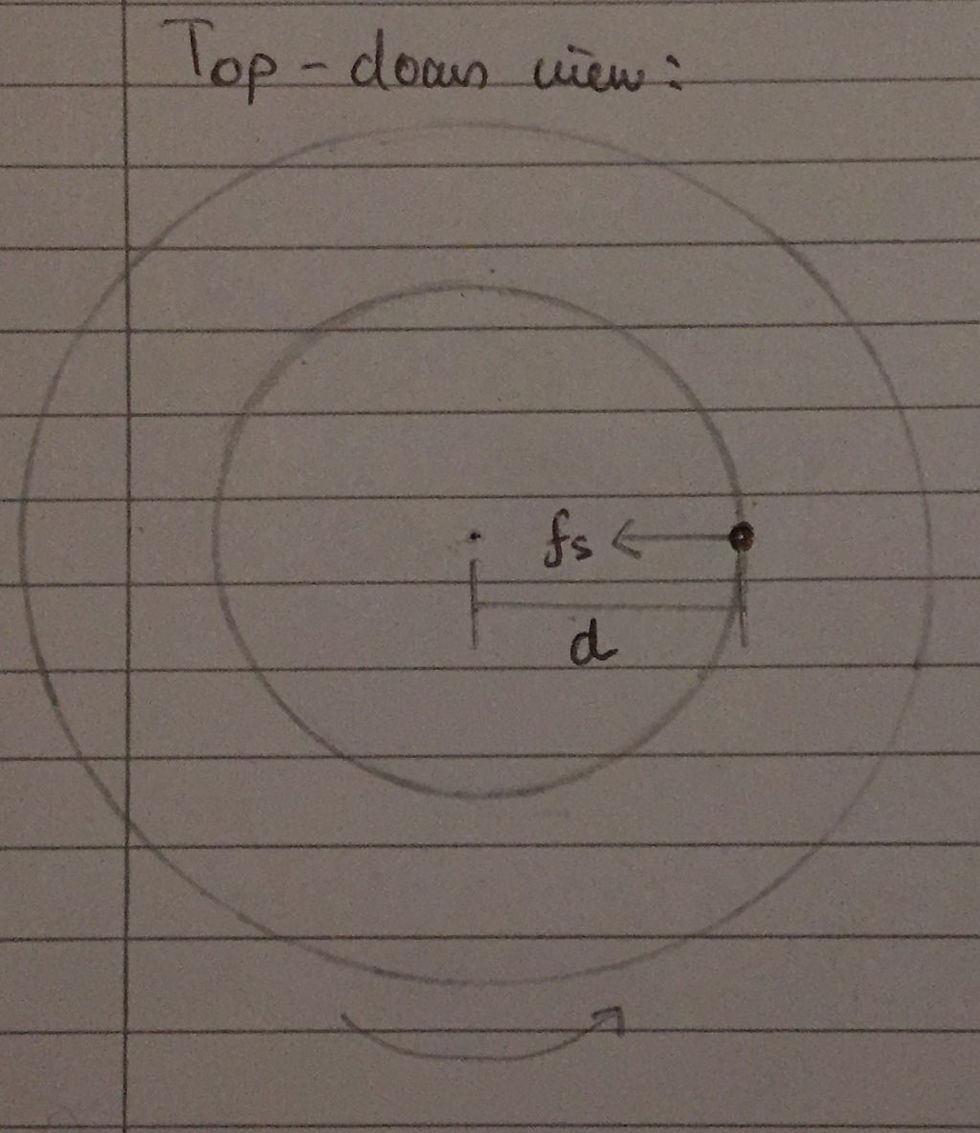
This question consists of a coin, with mass m, that is placed on a rigid disk. The coin is placed at a distance d from the centre of the disk, which is the radius of the coin's circular path. As specified in the question, there exists static friction between the coin and the disk, which I have labelled as Fs. Considering the problem from a top-down view, we can see that the only horizontal force acting on the coin is the static frictional force between the coin and the disk, labelled as Fs. This will therefore provide the centripetal force that acts on the coin, keeping it in circular motion, rotating anticlockwise relative to the centre of the disk, at a distance d away from it. I have included the top-down free body diagram above.

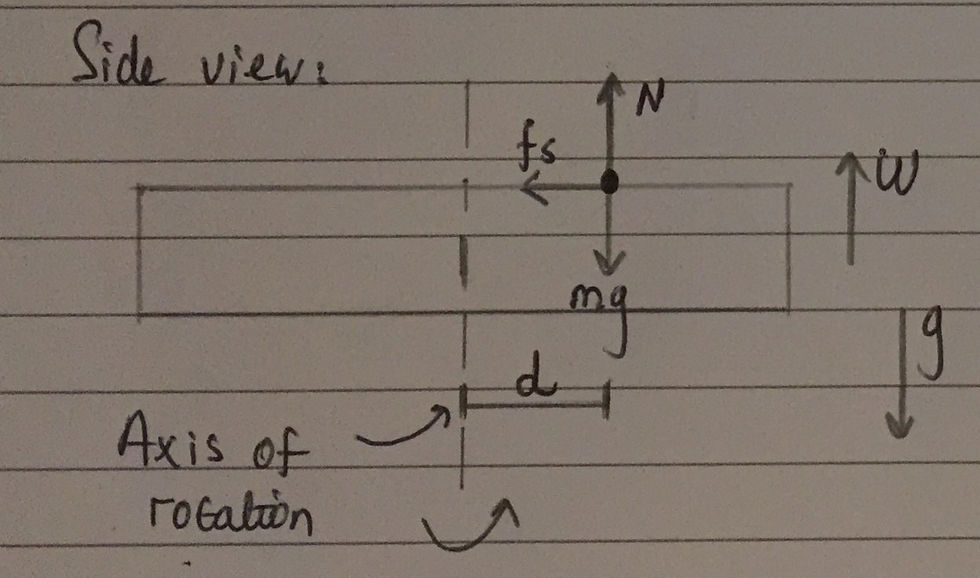
Considering the side view, we can yet again see that the static frictional force, Fs, is acting towards the centre of the disk and is the only horizontal force acting on the coin. In the vertical direction, the normal contact force between the coin and the disk, labelled as N, is equal to the weight of the coin, mg. I have included the side view free body diagram above.

Part A:

As aforementioned, the static frictional force, Fs, between the coin and the disk will provide the centripetal force which will ultimately keep the disk revolving around the centre of the disk for a certain period of time. We can therefore state that m*ω^2*d = Fs (1). The disk begins from rest, when t = 0, and, unlike previous circular motion problems that we have encountered in this problem set, it begins to rotate with a constant angular acceleration, indicated as α. This means that the coin will not rotate with a constant angular velocity, ω, but rather its radial velocity will increase as time increases. We know that angular acceleration, α, is defined as the rate of change of the angular velocity, ω, of a body with respect to time, t. In mathematical terms, dω/dt = α.

Thus by simple manipulation, we can state that dω = α dt. This allows us to integrate both sides, resulting in the following equation - ω = u + αt, where u is the initial angular velocity of the coin. The value of u in this case is zero as we are implicitly told that the disk rotates from rest. We can thus state that ω = αt (2). This is essentially the rotational equivalent of the translational equation of motion that is v = u + at. This can simply be memorised and used when necessary, however I believe it was beneficial to derive it in order to develop a greater appreciation of the mathematics behind the equations of rotational mechanics. I have included my workings in a diagram below:

In order to find the magnitude of the force of static friction between the disk and the coin as a function of time, Fs(t), we have to substitute equation (2) into equation (1) as I have done so in my calculations below:

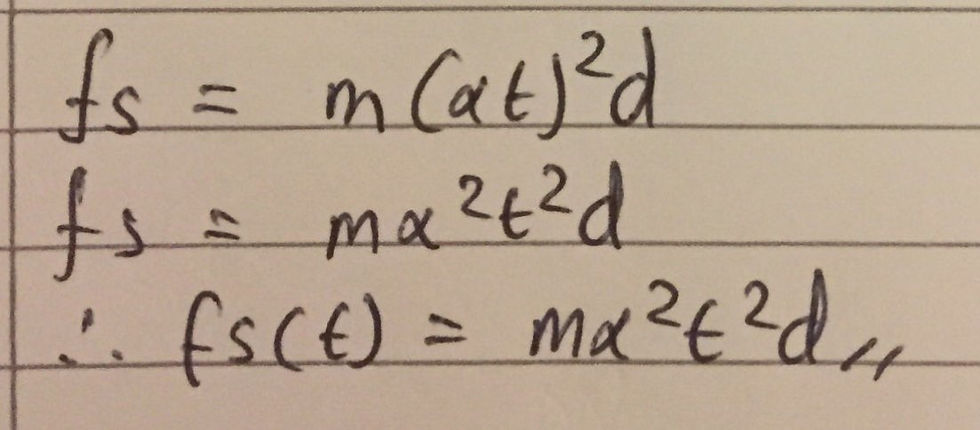
Part B:

As the angular velocity, ω, of the coin increases as time increases, so will the magnitude of the centripetal force that is required to keep the coin in circular motion. The centripetal force on the coin is provided entirely by the static frictional force, Fs, which is exerted by the disk on the coin. However, the static frictional force has a maximum value which is equal to μN, where μ is the coefficient of static friction between two surfaces - the coin and the disk in this case. Therefore, the coin will be on the point of slipping when the centripetal force acting on the coin is equal to the maximum static frictional force that can be exerted by the disk on the coin. In other words, m*ω^2*d = μN (1). We are not permitted to use N in our final answer. Resolving forces vertically, however, it is clear that N = mg (2). We can substitute equation (2) into equation (1). One now simply has to rearrange for ω, giving the final answer. I have included my final workings in a diagram below:

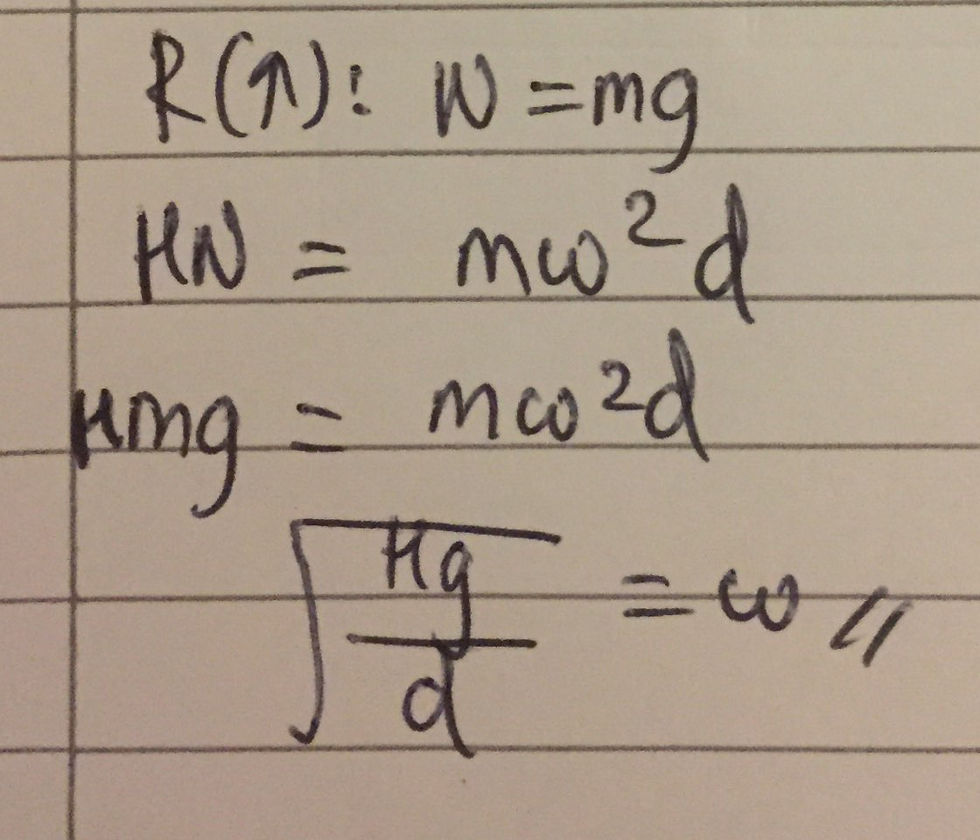
That is it for question six. If you have any questions about the problem, feel free to email us on the Contact Us page. That is the end of the solutions for Problem Set 3. I have very much enjoyed solving these problems and sharing my solutions with you all. If you would like me to solve any other problem sets, please comment down below.