Moment of Inertia - Derivation for a Slender Rod

Introduction

I remember when I first came across the idea of rotational mechanics while solving problems on a website called IsaacPhysics (if you haven’t heard of it, I strongly recommend checking it out). I instantly found the fact that there are rotational (angular) equivalents to translational (linear) quantities very interesting. Today, I will be focusing on the concept of moment of inertia, which can be viewed as the rotational equivalent of mass.

Moment of Inertia

The definition for moment of inertia is an object's resistance to rotational acceleration. The moment of inertia, I, of an extended object about an axis is defined as the summation of the mass x radius^2 for all the particles that make up the body. This can be written as a summation (in Sigma notation) as shown in the included photo below (where n represents the number of particles that make up the body):

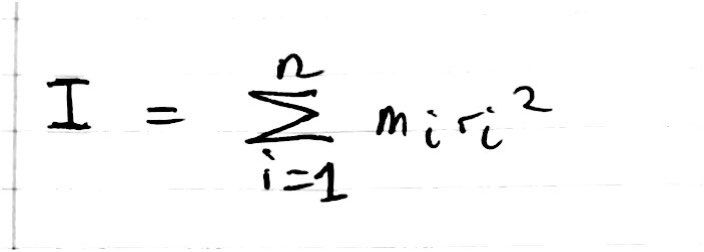
However, a more accurate definition involves integration. We can consider an object as being composed of an infinite number of small masses, dm, which are each a distance, r, away from the axis of rotation. Therefore, the moment of inertia about the axis of rotation can be given by an integral, with respect to dm, as shown in an image below (keep in mind that I have shown an indefinite integral but, when deriving an expression for the moment of inertia of a specific body, I will use the necessary lower and upper limits):

Moment of Inertia Derivation - Slender Rod

I will now derive the respective equation for the moment of inertia for a slender rod. As can be seen in my image below, the rod is of a length, L, with the axis of rotation being a distance, d, away from one end (I just randomly chose one, this does not matter).

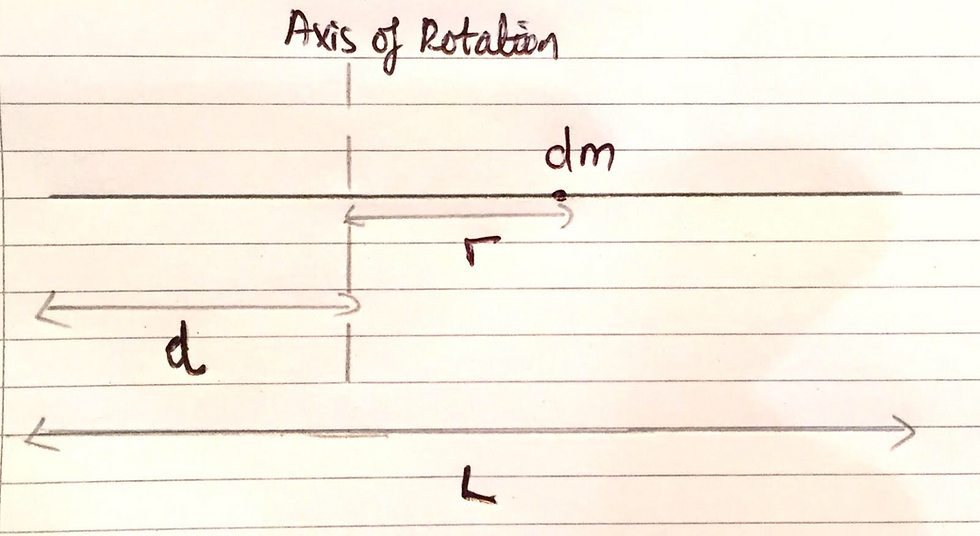
We know from our previous definition that the moment of inertia for a body is the summation of an infinite number of small masses, dm, which are each a distance, r, away from the axis of rotation - which can be represented as an integral of r^2 with respect to dm. Taking the axis of rotation as the origin, per se, the limits of the integral will become L-d and -d, as I have shown below:

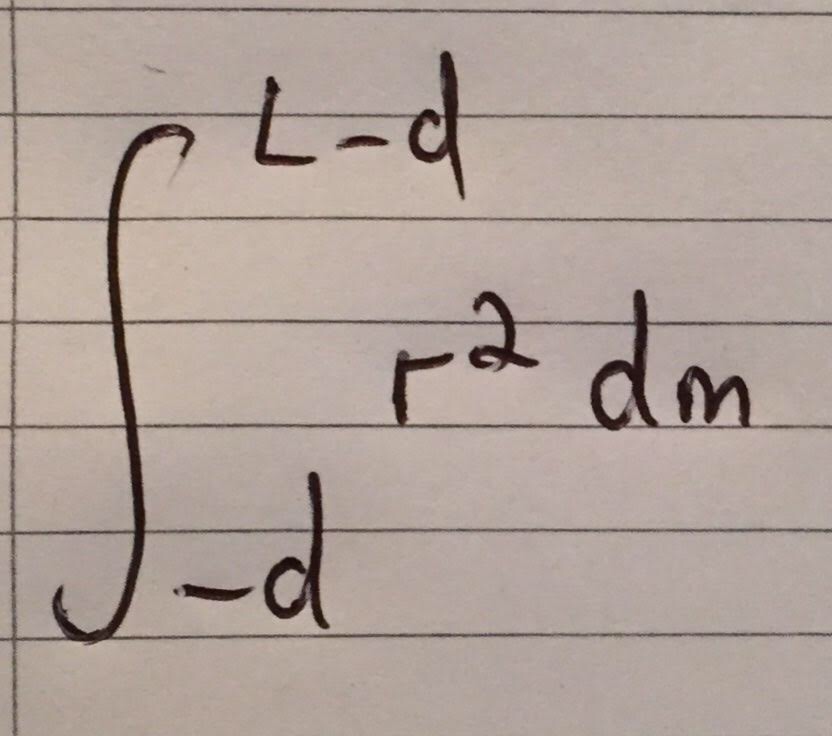
The problem is that we can not integrate the above expression as we must have dr instead of dm. Since the rod is modelled to have a negligible thickness, we can think about an infinitesimal mass element as being equal to the linear density, ρ, of the rod multiplied by dr, an infinitesimal length. We can also use the fact that the linear density, ρ, can be represented as M/L, where M is the total mass of the rod. Substituting this expression for dm into our integral should give the integral pictured below:

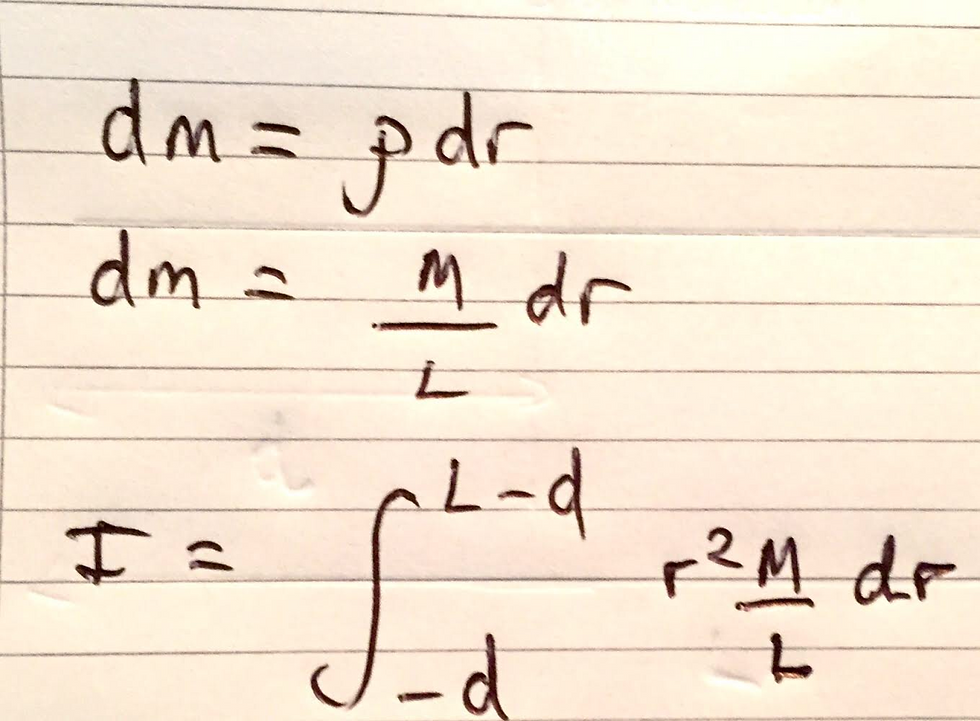
From here we integrate as we normally would and clean up the expression. As M/L is a constant, you can take it out of the integral. I have included an image of this below:

Integrate the expression as you normally would.

Substitute in the limits, expand and simplify as necessary.

This results in the general expression for the moment of inertia for a slender rod, with the axis of rotation being a distance, d, from the left end of the rod (as aforementioned, you can just as easily choose to measure this distance from the right end of the rod). For example, if the axis of rotation was halfway between each end of the rod, you could substitute d=L/2. You would then obtain the specific equation for the moment of inertia of a slender rod, with the axis of rotation through the centre of the slender rod. I have shown this below:

Remember you can only use this when d=L/2.

That is it for this post! Thank you very much for reading, and please feel free to ask any questions that you may have in the comments below. Stay tuned as I will be deriving the moment of inertia for increasingly complicated shapes. Next up will be a solid cylinder!