Moment of Inertia - Derivation for a Solid Sphere

Introduction

Hello and welcome to the third post on deriving the moment of inertia equations for different shapes. If you haven't yet read my post on deriving the moment of inertia for a slender rod or a cylinder, then please do. This post will build on the information that I have explained in the first two posts. This is a relatively difficult derivation so do not be afraid if it takes you a while to understand it.

Moment of Inertia Derivation - Solid Sphere

I will now derive the respective equation for the moment of inertia of a uniform, solid sphere. I have defined the solid sphere to have a radius of R and a mass of M. The axis of rotation is through the centre of the sphere. I have included an image of this below:

A diagram showing the solid sphere that we are considering.

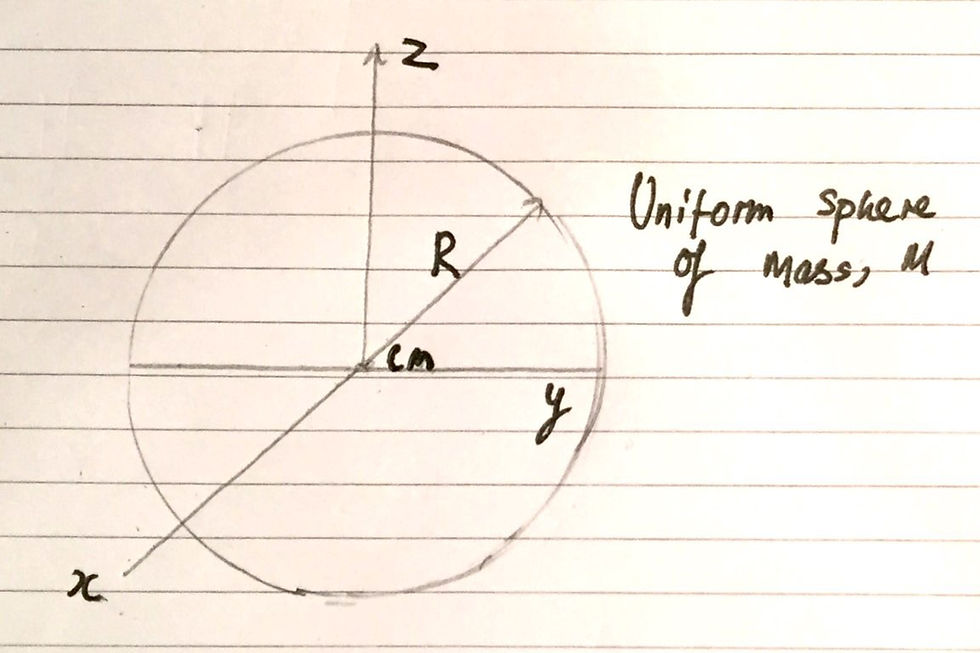
Our general integral for the moment of inertia is still the same as in the previous derivations. I have included an image below to remind ourselves:

General indefinite integral for the moment of inertia of a body.

We will now consider the moment of inertia of the sphere about the z-axis and the centre of mass, which is labelled as CM. If we consider a mass element, dm, that is essentially a disc, and is about the z-axis, it's radius squared, r^2, will be equal to x^2 + y^2 - this is using Pythagoras' theorem. Thus, we can substitute this value for r^2 into our integral, to calculate the moment about the z-axis, relative to the centre of mass, CM, as I have included in an image below:

Diagram used to calculate the moment of inertia of the sphere about the z-axis.

Indefinite integral for the moment of inertia about the z-axis.

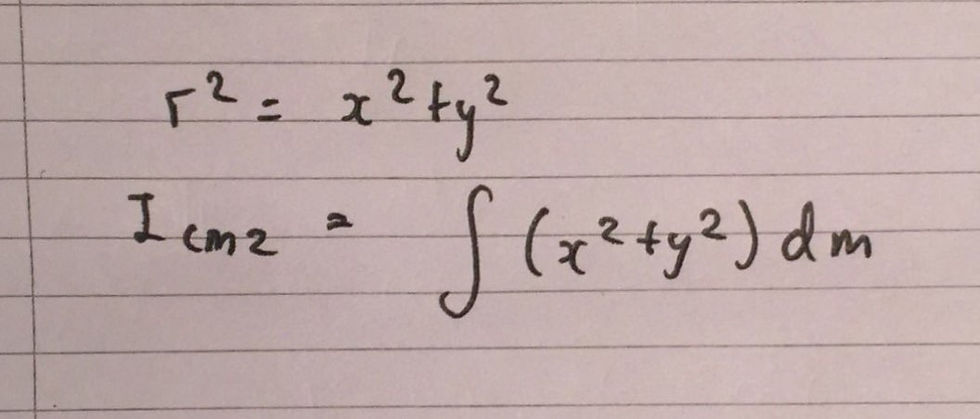
We can now apply the same principle to calculate the moment of inertia about the x-axis and y-axis respectively. I have included the following integrals below:

Indefinite integrals for the moments of inertia about the x-axis and the y-axis, respectively.

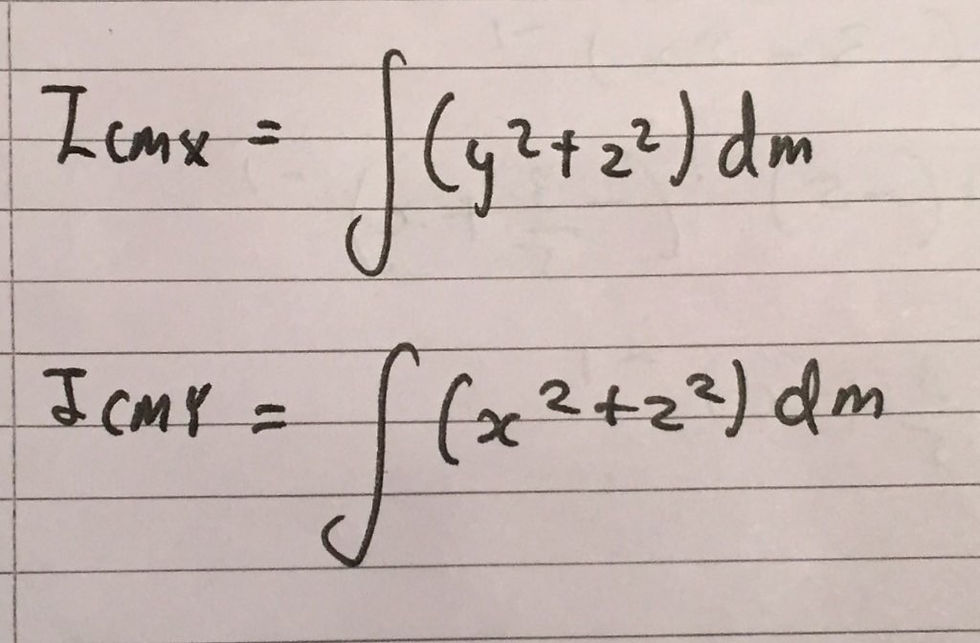
You may ask why this is all relevant to deriving the moment of inertia for a solid sphere. By the symmetry of the sphere, it should be apparent that all the three integrals, and therefore moments, are equal and will therefore respectively give us the overall moment of inertia that we are looking for. However, each integral contains the different variables, x, y and z, which make each integral very messy. We can counter this by simply stating that the sum of each respective integral will give us the three times the moment of inertia for the solid sphere, about the central axis. I have included this in an image below:

Expressing the moment of inertia of the solid sphere in terms of x,y and z.

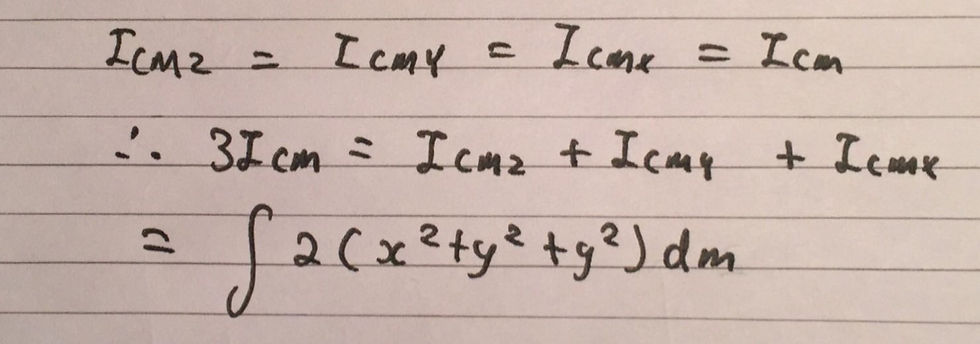
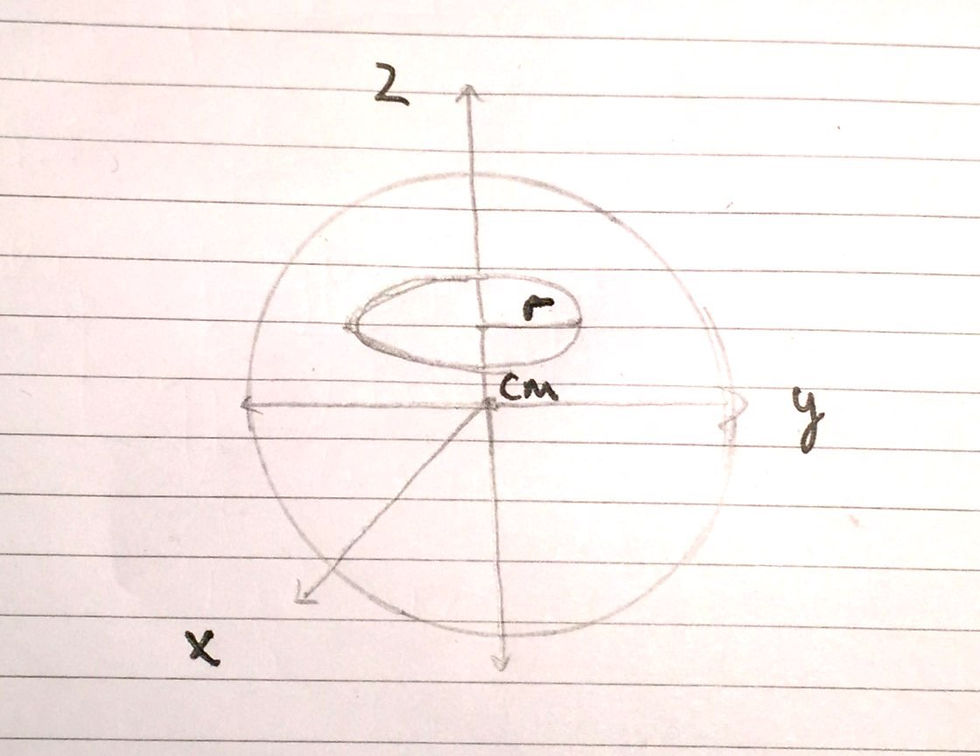
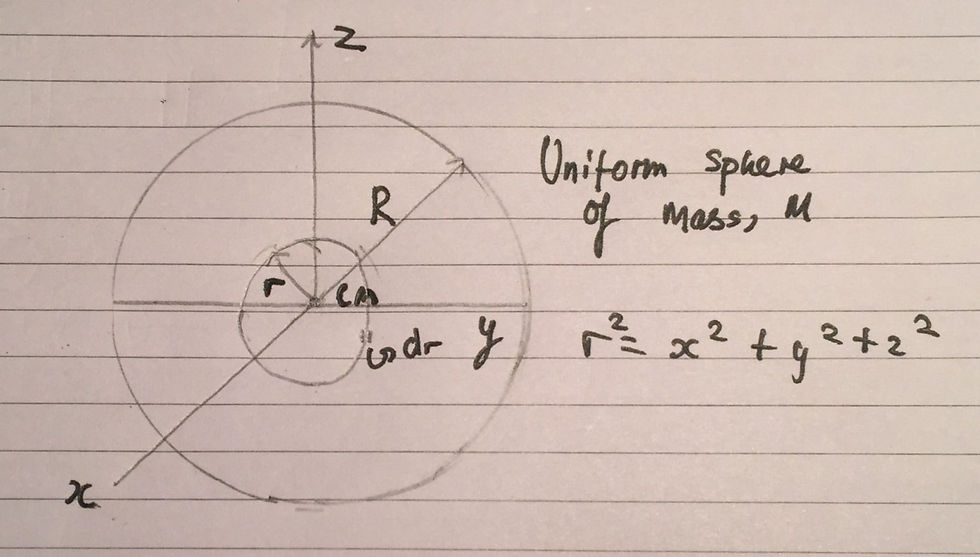
From here we can visualise that x^2 + y^2 + z^2 is the radius squared , r^2, of a small sphere of thickness, dr and mass dm. We can therefore alter our initial diagram for the sphere to include this - I have included this in an image below:

Considering an infinitesimally small, thin sphere, with thickness, dr, and mass, dm.

Expressing the moment of inertia for a solid sphere in terms of r.

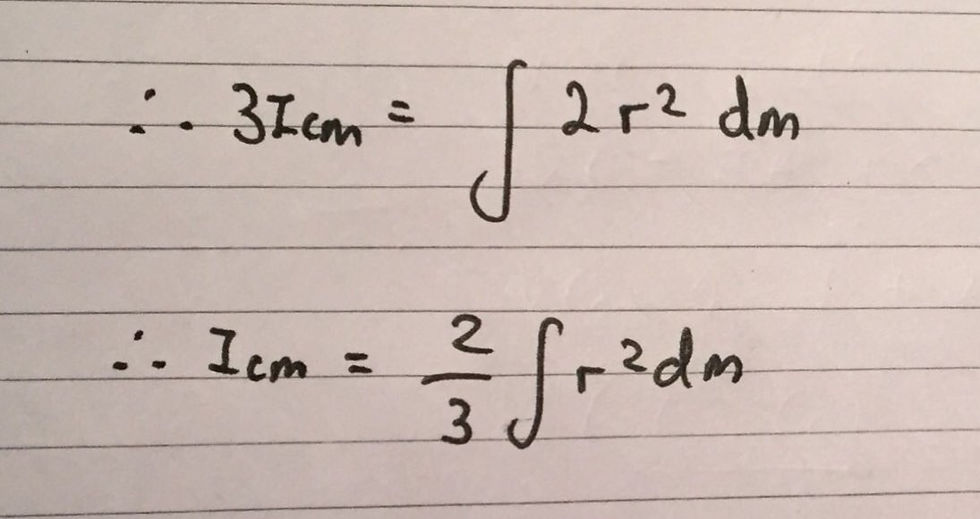
As in every derivation, we must now create an expression for the mass of the sphere, dm, in terms of dr, as this will allow us to evaluate our integral. We can express dm as being equal to the volume density of the sphere, ρ, multiplied by the volume of the thin, small sphere, which is simply dV. I have included this expression in an image below:

Expressing dm in terms of dV.

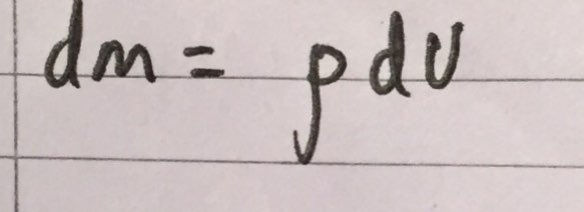
We can therefore put, ρ, in terms of the radius of the entire sphere, R. We can also express the volume of the small sphere, dV, in terms of r, the radius of the small sphere. This is simply equal to 4πr^2, which is the surface area of the inifinitesimally thin sphere, multiplied by its thickness, dr. We can thus substitute these respective expressions into our integral. I have included an image of this below:

Expressing dm in terms of dr.

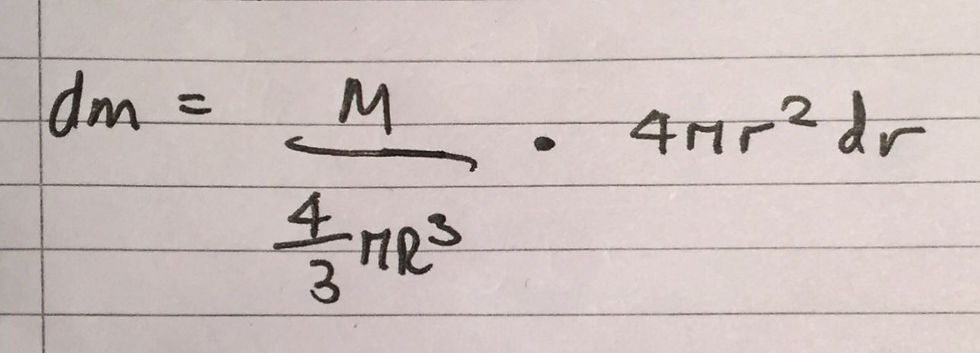
This allows us to use algebraic manipulation to clean up the integral, as I have included below:

Simplifying the integral.

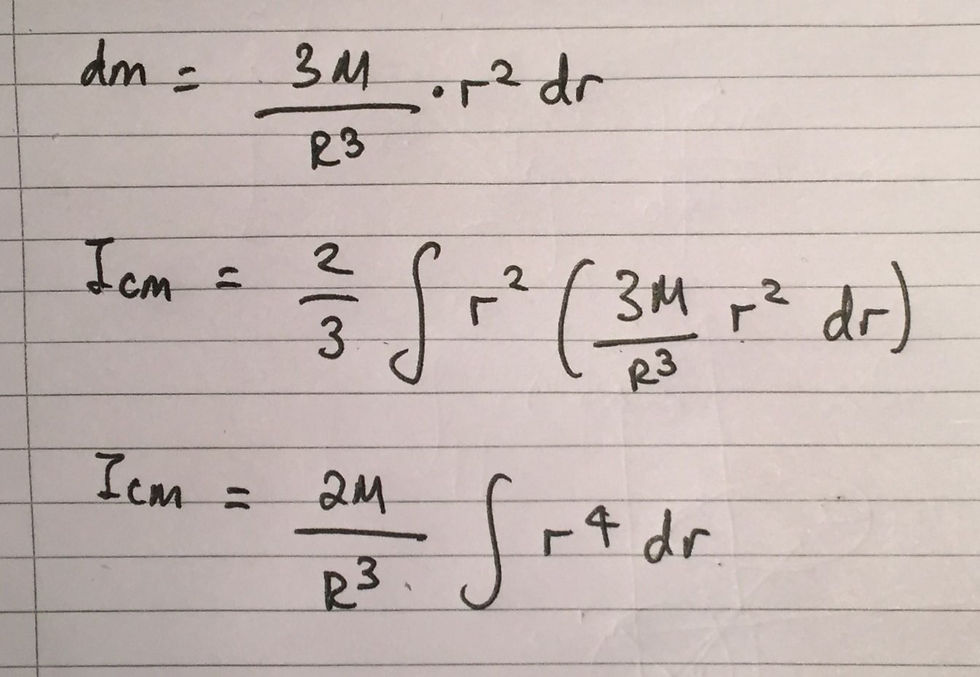
From here we can set the limits of our integral as 0 and R and can evaluate our integral. I have included this in an image below:

Evaluating the integral.

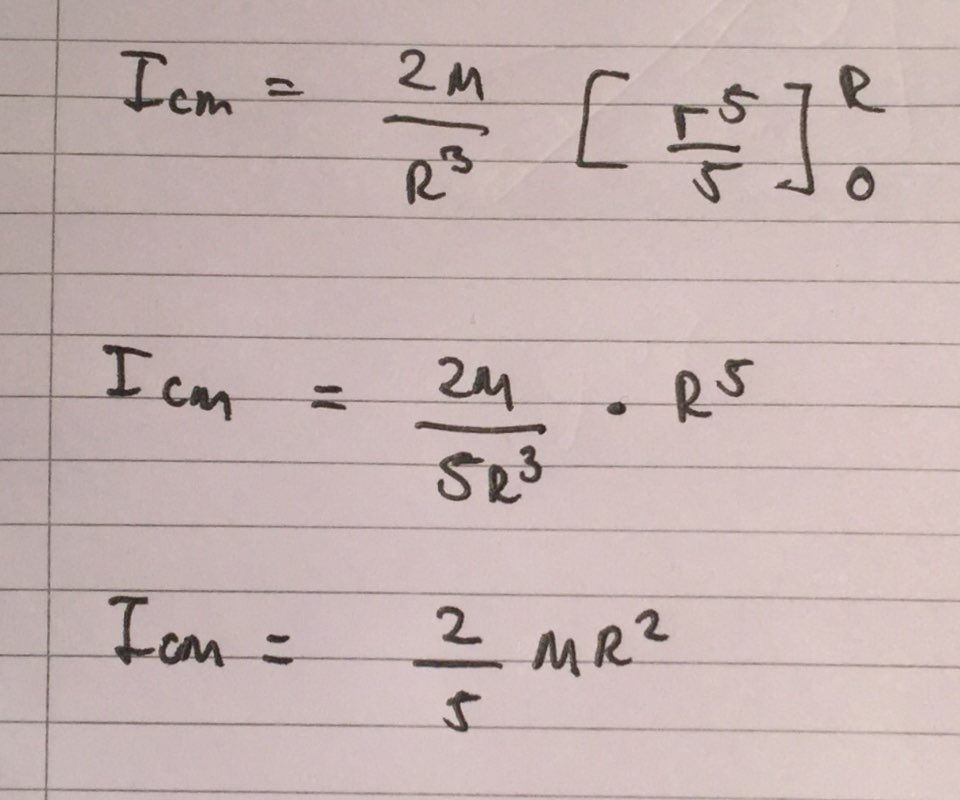
This gives us a very neat final answer for the moment of inertia of a solid sphere, with the axis of rotation through its centre of mass. I have included an image of this below:

Et voila! This is the moment of inertia for a solid sphere.

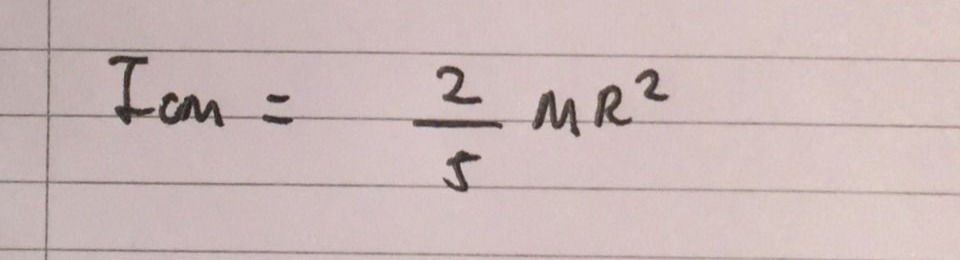
That is it for this derivation! I might continue deriving the moments of inertia for different shapes, however I am planning on creating a new 'series'. As part of my revision for A-Level Physics, I have derived a lot of the equations that are used within the specification as this allows me to develop a better appreciation for the fundamental physics behind each equation. Thus, I am planning on uploading some of the more 'interesting' derivations, to share this knowledge with you. Feel free to comment on which derivation you would like to see in particular. Thanks for reading this post and stay tuned!