Quickest Way to Lose Weight Using Physics
- Joel Runevic

- Aug 14, 2019
- 7 min read
Updated: May 20, 2020
Introduction:
Before I begin, I want to explain that this is not a method of actually losing 'weight' in the conventional sense but rather I decided to have a bit of fun with weighing scales, creating a little experiment involving mechanics. While reading my physics textbook, I discovered the principle behind how a weighing scale works. Before beginning, it is important to be able to understand the difference between 'mass' and 'weight'. Mass can be defined as a measure of the amount of matter in an object or as a measure of an object's inertia, which is its resistance to change of motion. More force is required to give an object a certain acceleration than to give an object, with less mass, the same said acceleration. Weight, on the other hand, is the force of gravity acting on an object and therefore depends on the strength of the gravitational field that the object exists within, as well as its mass - w = mg, where m is the mass of the object in kilograms and g is the strength of the gravitational field that the object is within. For example, an object placed on Jupiter would have a larger weight than if the same object was placed on Earth. On the other hand, the mass of the object would remain constant, regardless of where the object is positioned.
The weight of the object on the scale is not directly measured per se but rather it is the force that is exerted on the object by the weighing scale. When placed on a horizontal floor, and the system is in equilibrium, resolving vertically, one can see that the weight of the object must be equal to the force that the weighing scale exerts on the object, otherwise known as the normal reaction force on the object. I have included a diagram showing this below (mg represents the weight of the object and N denotes the normal reaction force on the object).
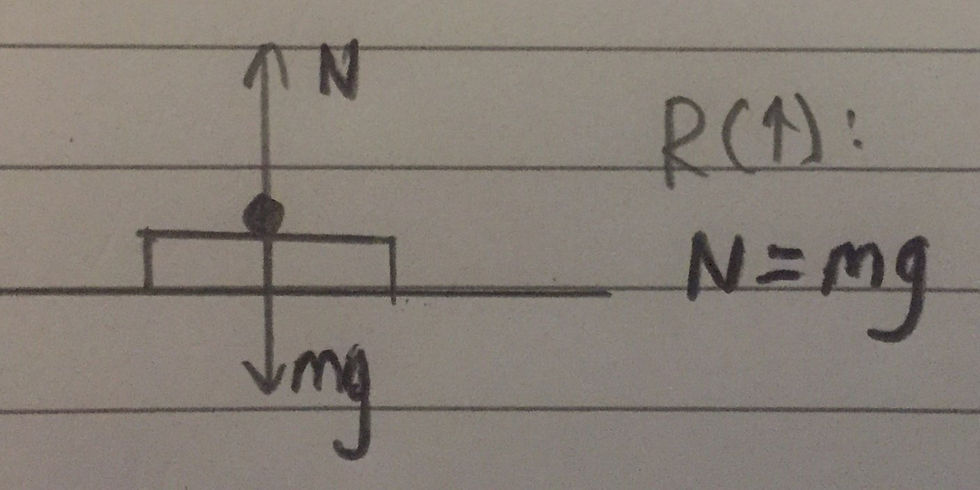
This is where Newton's Third Law comes in handy. This states that 'when two objects interact, they exert equal and opposite forces on each other'. A common misconception, however, is the idea that the weight of the object and the normal reaction force exerted on the object are a pair of equal and opposite forces that arise due to Newton's Third Law (otherwise known as action-reaction force pairs) - this is not the case. The normal force acting on the object, exerted by the weighing scales, is equal and opposite to the force exerted by the object onto the weighing scales - this is an action-reaction force pair.
The weight of the object is therefore equal and opposite to the gravitational force exerted on the Earth by the object (the person standing on the scales in this case). The mass of an object can be thought to create a force field around itself. Any other mass placed in the field is attracted towards the object. This said second mass also has a force field around itself and therefore pulls on the first object with a force that is equal in magnitude but in the opposite direction. However, the mass of the object is negligible relative to the mass of the Earth and therefore we cannot see the effects of the gravitational force exerted on the Earth by the object. By the same logic, the gravitational force exerted on the object by the Earth, what we call the object's weight, is noticeable as the mass of the Earth is much larger than the mass of the object - this is the force that causes objects to fall down towards the Earth when they are dropped.
As aforementioned, when the floor is horizontal, the normal reaction force acting on the object must also be equal to the weight of the object. This force is then converted to the mass of the object by dividing the force by g, the gravitational field strength of the Earth (9.81 N/kg), and the weighing scale displays the final mass of the object.
This got me thinking as, by simple mechanics, it can be shown that the normal reaction force exerted onto the object by the weighing scales decreases in magnitude when the weighing scales are inclined at an angle, labelled as θ. By resolving forces vertically, the normal reaction force, N, can be shown to be equal to mgcosθ. There will also be static frictional forces between the object and the weighing scale, as well as the weighing scale and the inclined plane, denoted as F1 and F2 respectively. However, these forces are parallel to the slope and are thus perpendicular to the normal reaction force and will have no effect on the displayed mass of the object. I have included a diagram below:
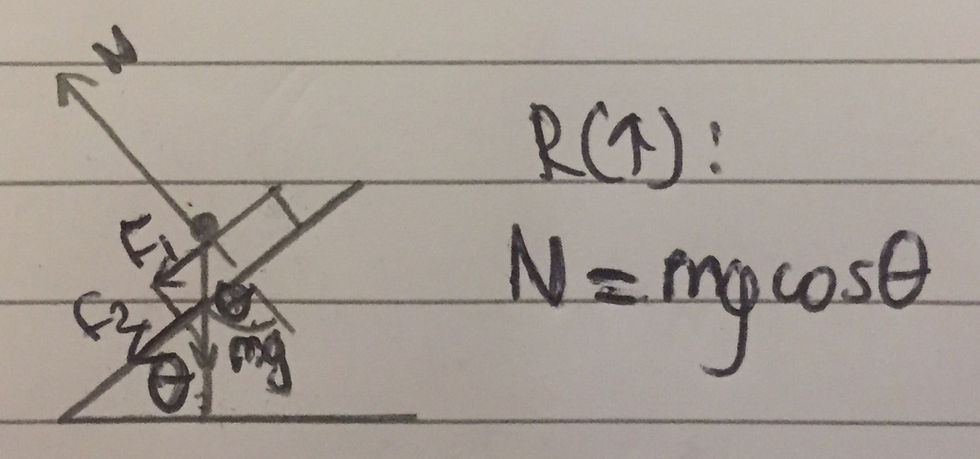
I have also included an image of the cosine graph below, with the domain 0 ≤ θ ≤ 90, where θ is in degrees, as this is the range of angles that we are interested in.
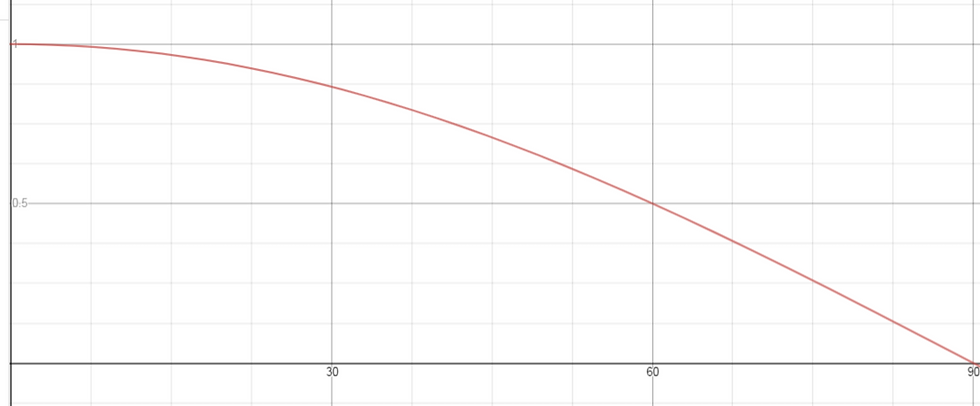
As can be seen, the value of cosθ decreases, at an increasing rate, as the value of θ increases from 0 to 90. Therefore, the normal reaction force, N, exerted onto the object also decreases in magnitude as θ increases. Consequently, the force exerted onto the weighing scales by the object also decreases in magnitude, as they are an action-reaction force pair. The weight of the object is unaffected and remains at mg in magnitude. Thus, theoretically, the weighing scale should display a mass that is less than the 'actual' mass of the object, but is instead equal to mcosθ, where m denotes the 'actual' mass of the object in kilograms (there is no g as, to calculate the 'apparent' mass, one has to divide by g).
Experiment:
I now have a hypothesis that I can test. The 'apparent mass', which I will denote as M, (that is the mass that is displayed on the weighing scales) can be modeled as a function of θ like so: f(θ) = mcosθ. In other words, I am predicting that I will be able to empirically prove that M = mcosθ where 0 ≤ θ ≤ 90. The method I will be using will not be 'scientific' by any means, as this is simply an investigation I have completed at my home, utilising any equipment I can find around the house.
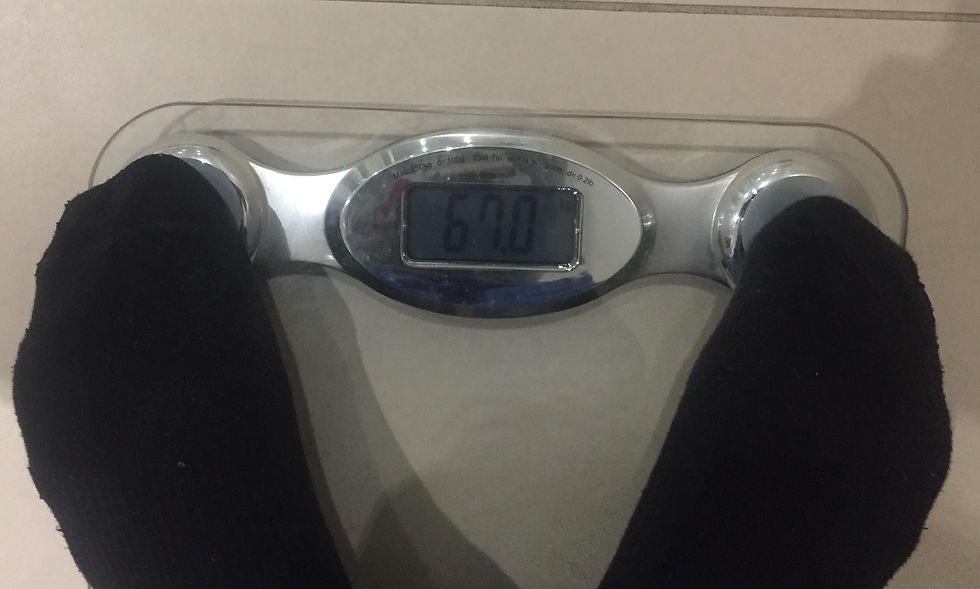
Firstly, I had to find out my mass, when θ is 0. In other words, this is my 'actual' mass that is displayed when the weighing scale is positioned on a horizontal floor. I would therefore be able to find out m. I did this 5 times in order to be able to discard any anomalies as well as so that I would be able to calculate a reliable and accurate mean average. This came out to be 67.0 kg. In fact, every reading was 67.0 kg, suggesting that the weighing scale is very precise (there is very little variation in readings). I have included an image of the electronic weighing scale below:
In order to incline the weighing scale at an angle, θ, I will be creating a stack of books, allowing me to incline one end of the scale onto the stack of books and the other end will remain on the floor. However, this means that the weighing scales will only have two points of contact with the inclined plane, rather than having a continuous point of contact with the floor, per se, when placed horizontally. Despite this, I doubt this will affect the results as the weighing scale is measuring the net force that the weighing scale exerts onto my body. I will calculate the angle θ through using simple trigonometry. I will measure, using a ruler, the vertical distance between the floor and the elevated end of the weighing scale, which I will call distance a. Subsequently, I will measure the horizontal distance between both ends of the weighing scale and will denote this as b, using a set square to ensure accurate measurements. I will then be able to calculate θ as arctan(a/b) = θ. I will repeat each reading 5 times, calculating an average.
I have included an image of the weighing scales inclined at an angle to the plane, below:

I have also included an image of the second reading of when the weighing scales were inclined at an angle of 27.5 degrees to the plane, below:

I have also included my results table below:
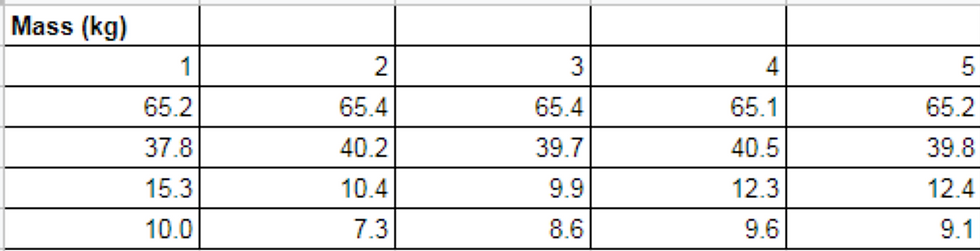
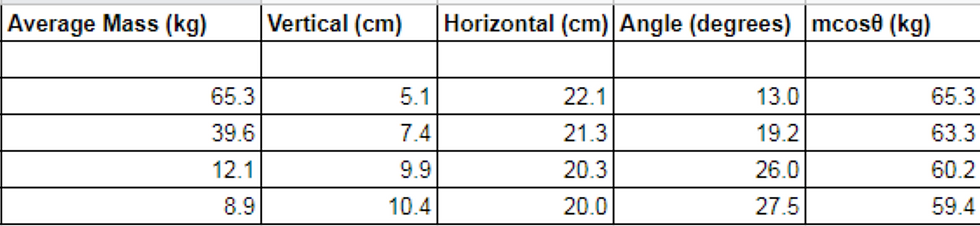
Analysis of results:
When the weighing scales were inclined at an angle of 13.0 degrees, the average 'apparent' mass was 65.3 kg (to 1d.p). This is identical to the value predicted by my hypothesis that M = mcosθ (to 1d.p). However, it is clear that this hypothesis breaks down immensely when the value of θ increases. I could only do the experiment until the angle was 27.5 degrees, as at angles greater than this, the weighing scales did not display a mass. I plotted the points on Excel to calculate a potential, alternative relationship between M and θ and included my findings below:
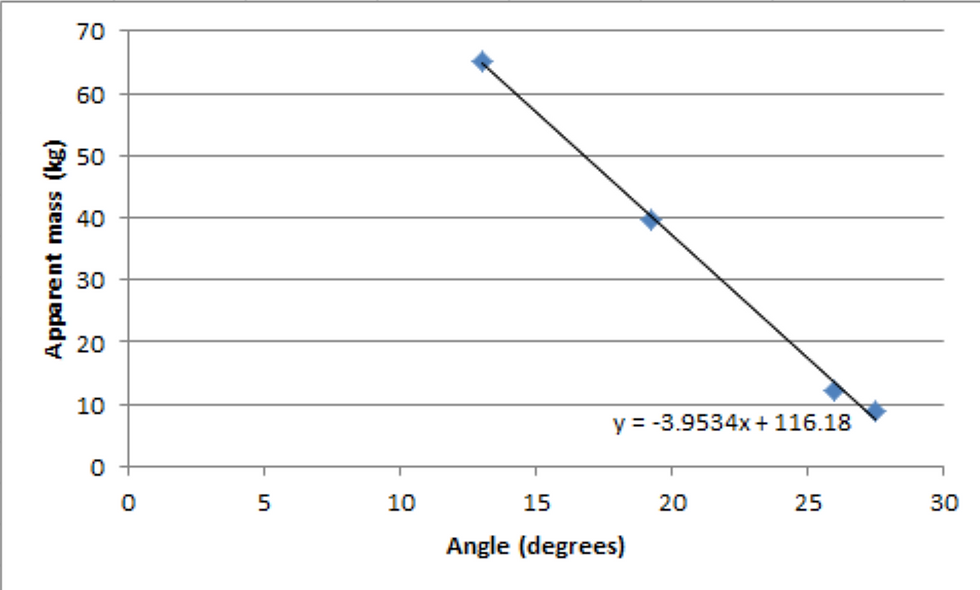
Clearly, based on my data, the relationship between the 'apparent' mass, M, and the angle of inclination, θ, is a linear one and not a trigonometric one like I predicted. However, I believe that my methodology was flawed and not my hypothesis. I made the assumption that despite the fact that the weighing scales are in contact with the floor at two 'discrete' places and not continiuously, the overall normal reaction force would be the same as if the weighing scale was inclined on a plane and not elevated. In hindsight, this was a flawed assumption to make as the weighing scale would be in contact with two different surfaces and would thus have two separate normal reaction forces - leading to the inaccurate measurements that can be seen in my results table. Moreover, I believe that another reason for the unexpected results was the fact that at each corner of the digital scale, there is a pressure sensor. However, when elevated, a smaller proportion of the pressure sensor is in contact with the plane, which could be responsible for the drastic decline in the 'apparent' mass, M, that is seen when the angle of elevation, θ, increases.
All in all, I am very glad that the 'apparent' mass, M, decreased when the angle of elevation, θ, increased as I predicted using mathematical reasoning. My next aim is to adapt my method, finding a way to incline the weighing scale on a plane rather than elevating it, in order to see if my hypothesis is truly correct or incorrect. Stay tuned for the second post on this experiment!



Comments