The 5 Hardest ACT Math Questions Ever
- Joel Runevic

- Sep 13, 2020
- 12 min read
Welcome to a post on the hardest ACT Math questions ever. We will be going through the five hardest questions that I could find regarding the ACT Math Section. If you aren’t aware, the ACT, like the SAT, is a college admissions test that High School students can choose to sit in order to progress to university. Unlike the SAT, the ACT is much more about how you are able to manage under time pressure. On the other hand, the SAT tends to have more challenging Math Questions. For example, I recently wrote an extensive post on arguably the hardest ever SAT Math Question. Make sure to have a look as it is advised to take both the ACT and SAT in order to see what is best for you!
Let’s have a look at the first question then.
Question One
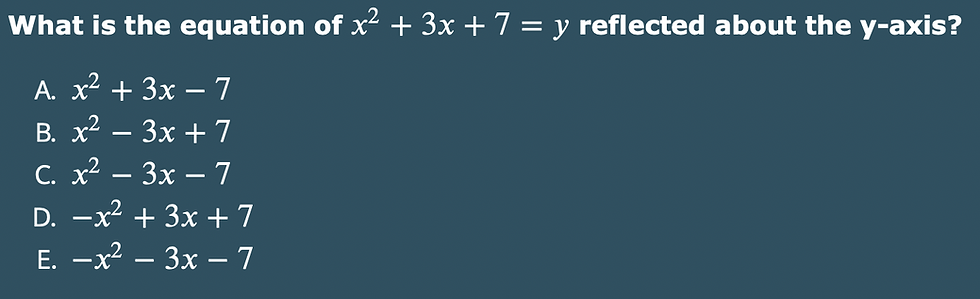
Most people will look at this question and immediately think of plotting the graph on their graphical calculator - the ACT Math does allow the use of a calculator and a graphical calculator is recommended. So, going along with how the majority of test takers would attempt this question, let’s have a look at a plot of the graph below.
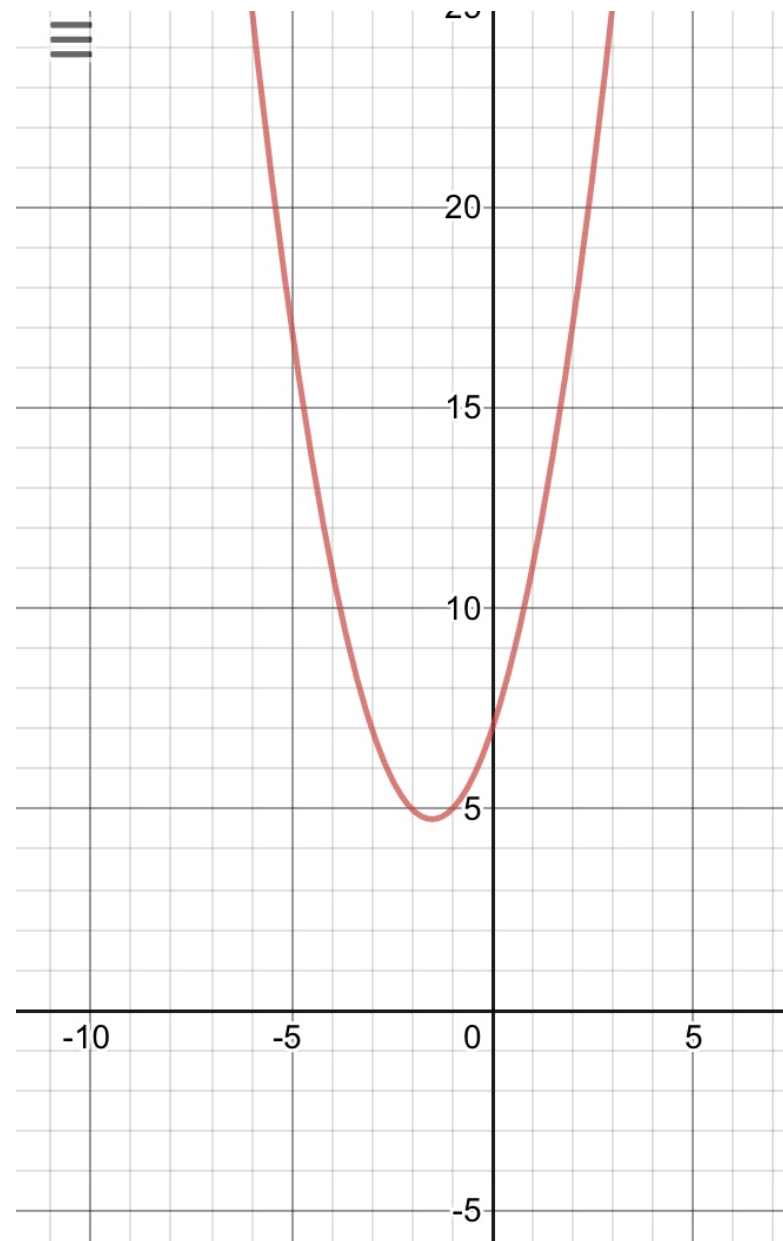
Above is a graph of y = x^2 + 3x + 7. By analyzing the graph, we can tell that the y-intercept will remain exactly the same if the function is reflected in the y-axis. So, the polynomial must have a value of +7 for ‘c’. By process of elimination, this leaves us with options B and D. We can also, by graphical reasoning, eliminate option D. This is due to the fact that a negative coefficient, in front of the x^2 term, will result in the parabola reflecting in the x-axis or, in layman terms, from becoming a U-shaped function to a N-shaped function. Clearly, this would not be the case if we just simply reflected the graph in the y-axis, and, indeed, the answer is B.
However, in my opinion, this is not a very effective or reliable method to answering such a question. In fact, there is a far easier and reproducible method to answering a question like this. All you need to remember is that for a function, f(x), the function that represents a reflection in the y-axis is simply f(-x). Therefore, you can simply substitute in -x into the original function and simplify to get the resultant function. This is a much quicker and mathematically sound solution as it does not rely on plotting a graph and then trying to eliminate multiple choice options. Remember, you are much better off solving the question and simply circling the option that supports your answer rather than trying to eliminate answer choices - only do this as a last resort!
If you don’t quite get what I mean, have a look at my solution for this problem. Look how much quicker it is:
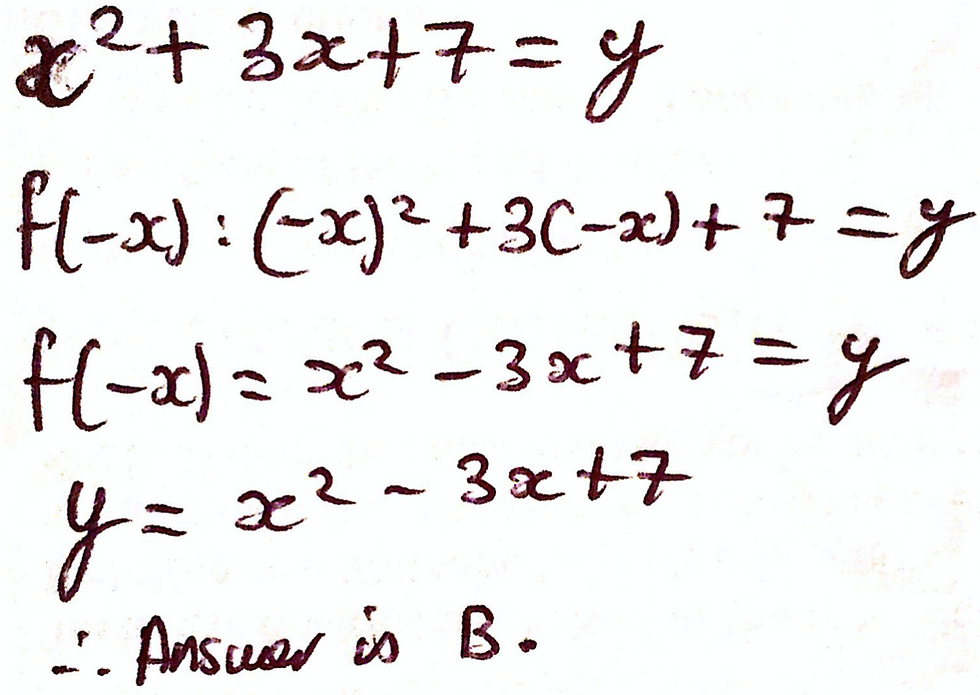
That was our first question out of the five that we will be completing in this post! You may be wondering, however, “what is the point of using your method if I can just plot the graph and use the process of elimination?”. The reason is that, firstly, it relies on you being able to discern between the incorrect answer choices and the correct answer. This may be possible with simple quadratic polynomials, but the ACT may chuck in some cubic or even quartic functions, making this method redundant.
Secondly, you are wasting precious time by plotting the graph and then trying to use it to figure out the correct answer. You are much better off simply substituting in -x and quickly simplifying the respective function. A 20 second saving on one math question could be the difference between scoring a 34 and a 35, or even a 36 - trust me, every second counts on the ACT.
Question Two
Here is a question that does involve using a process of elimination. Have a look at the image of the question below.
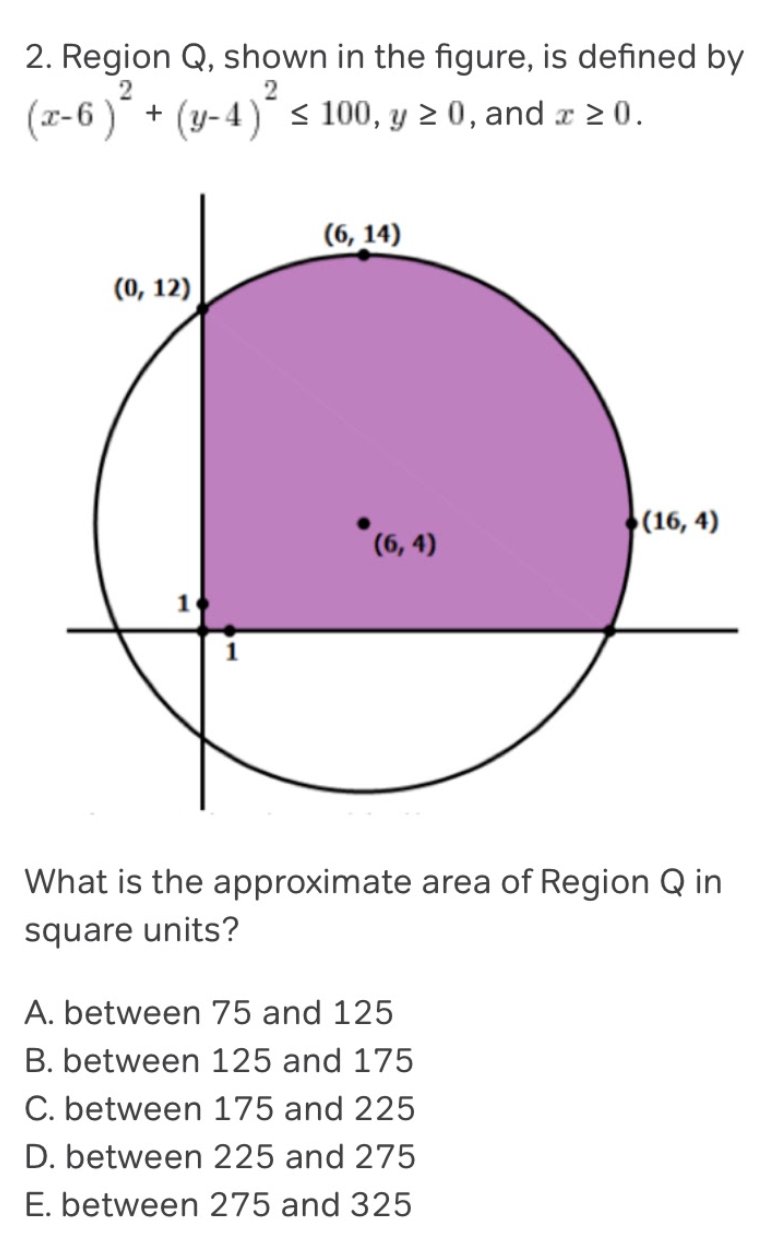
This is a challenging question if you don’t realise a nice little trick. The answer choices give intervals within which the area can fall within. Therefore, this is a good indicator that working out the actual area of the circle will take far too long and that we must simply find an accurate approximation for it.
Normally, you should aim to complete one ACT Math question per minute. However, this type of question (difficulty wise) will often appear in questions 55-60 and thus will require around 2 minutes to solve. However, if you didn’t realise that working out the actual area is unnecessary, you could take up to 5 minutes to solve this problem, likely costing you a total of 4 marks as you will not have enough time to finish other questions on the ACT Math Section. Thus, as aforementioned, saving 20-30 seconds on an easier question - like the first one we tackled in this post - can allow you to spend more time on the harder problems. Always make sure that before you start to solve a question, you’ve taken a few seconds to carefully think what it is exactly that you need to solve. In this case, we can simply approximate, which will save us so much valuable time. Let’s begin to approximate the shaded area of the circle!
The best thing we can do is to try and calculate the area of some shapes that roughly fit the shaded area of the circle. In this case, we will calculate the area of two trapeziums. Both trapeziums will slightly underestimate the shaded area. However, if we obtain an approximation that falls within an interval, we can be confident that this is the correct interval that the entire shaded area falls within.
The reason why I particularly selected trapeziums is because trapeziums are often used to approximate the area under a curve - in other words, trapeziums can be used to approximate the value of an integral. If you are interested, make sure to check out the trapezium rule.
Now, you may be wondering what trapeziums we should select. Essentially, you should use trapeziums that encompass the vast majority of the shape without requiring too much calculation to find the actual dimensions of the trapezium. Thus, in this scenario, one of our trapeziums could be bounded by the coordinates (0,0), (6,0), (6,14), and (0,12). The other can be bounded by the points (6,14), (6,0), (16,0) and (16, 4). Below, I have included an image of the original question but with our imaginary trapeziums highlighted.
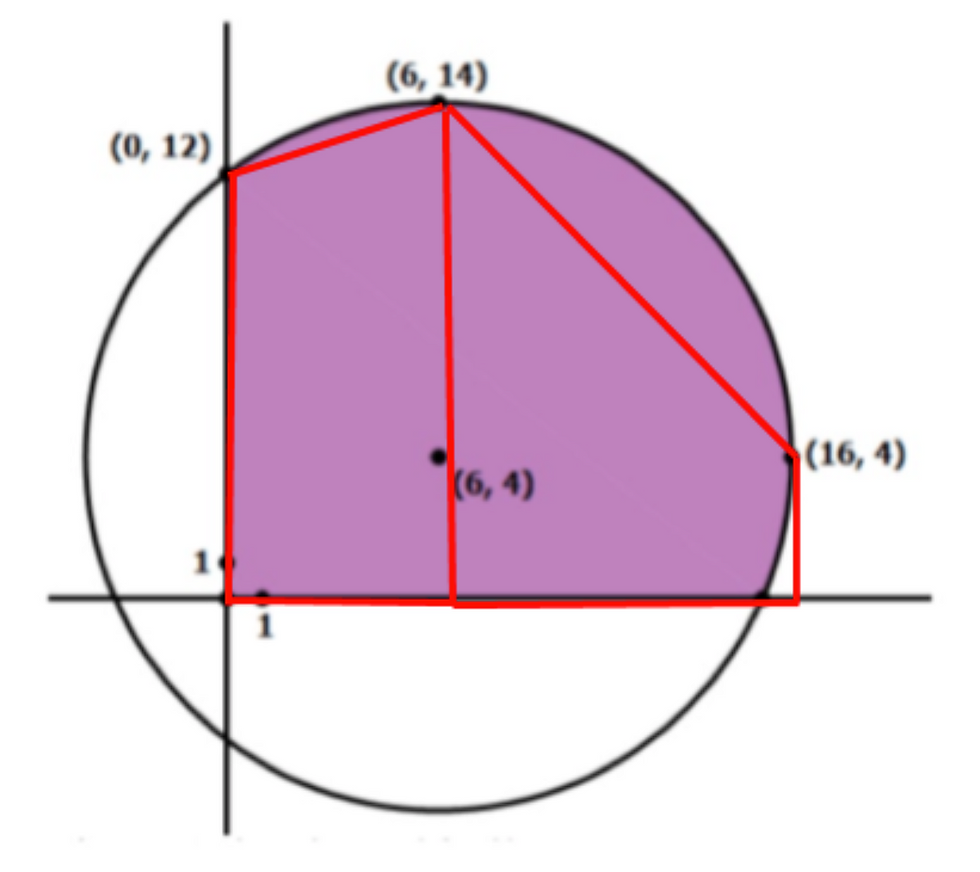
The two trapeziums that we will be calculating the area of are outlined in red. From here, we can begin to work out the area of each respective trapezium. If you aren’t aware (which you should be) the area of a trapezium can be calculated as follows. Note that h represents the perpendicular height of the trapezium:
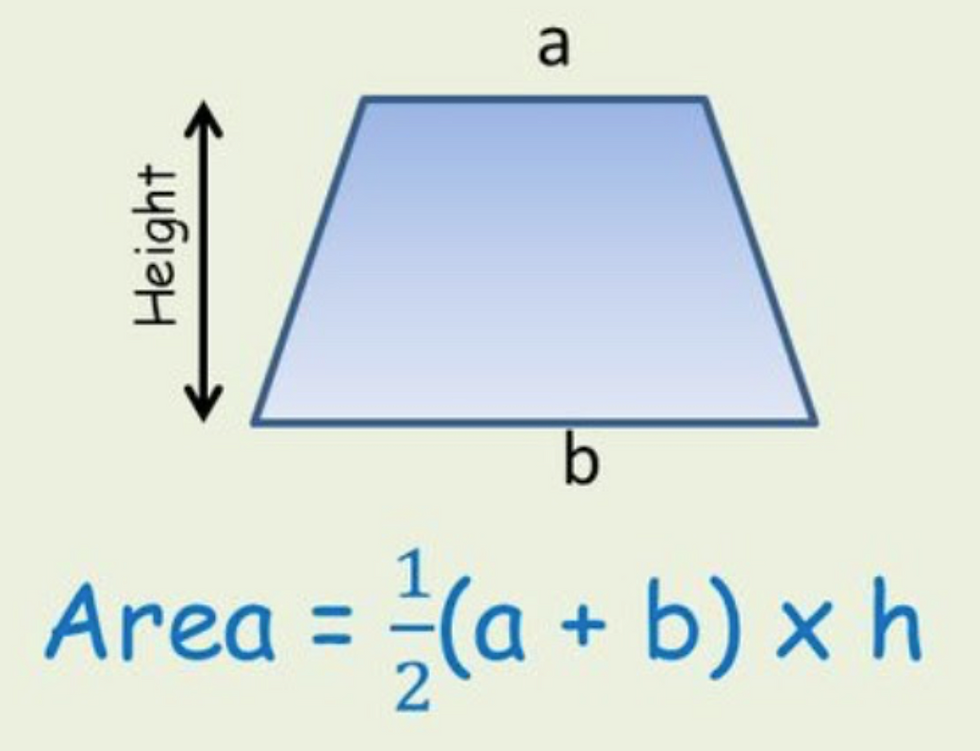
Thus, we can calculate the two respective areas of our trapeziums. I have included an image of this below.
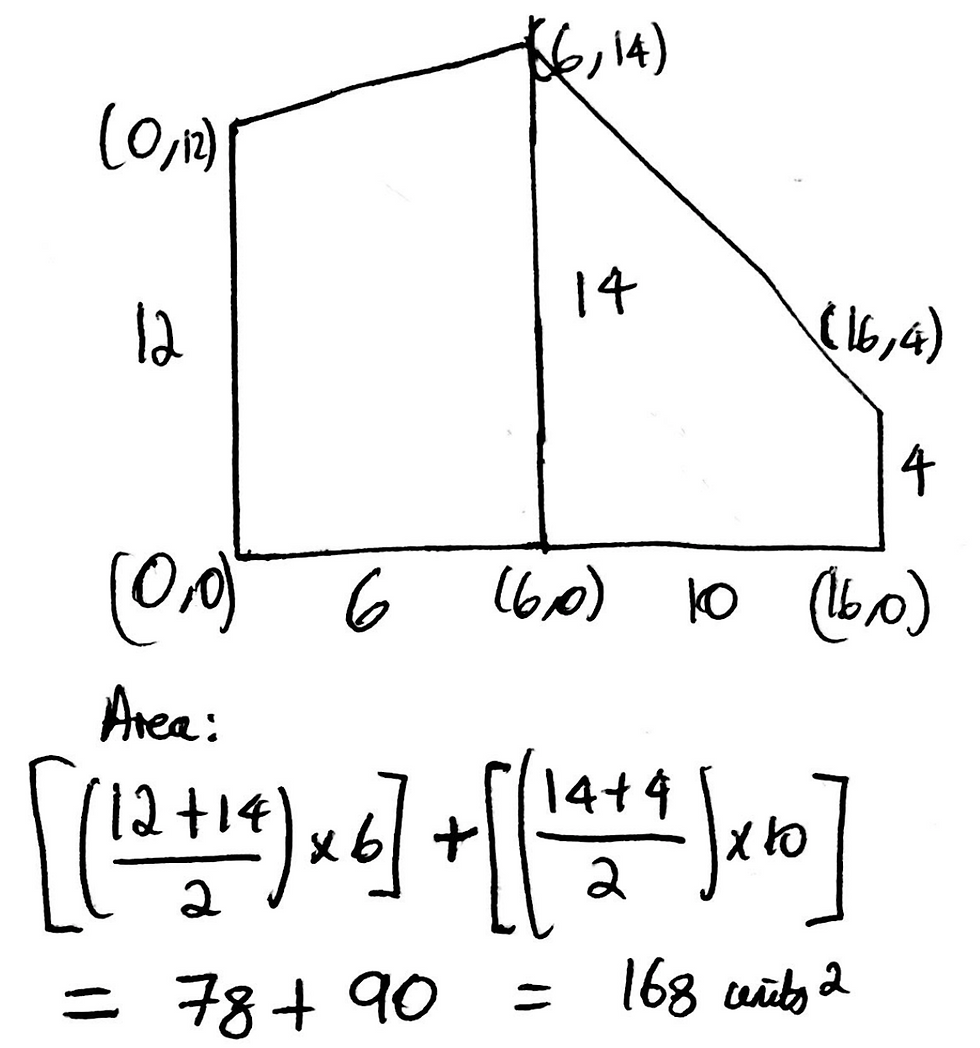
As can be seen from the image above, the total area comes out to be 168 square units. Thus, one may immediately say ‘ok so the answer is C, right?’. Not quite. Looking at the answer choices, we can see that B gives an interval of 125 and 175. 168 is very close to 175. Moreover, if we look at the shaded area of the circle that we did not incorporate into the trapeziums, although relatively small, it does not appear to be less than 7 square units. Remember, on the ACT, images are drawn to scale unless specified otherwise. Thus, we can take an educated guess that the area will be slightly above 175 square units but not by an immense amount. Therefore, it is very, very likely to be less than, say, 225 square units. With this in mind, if we look at the answer choices again, we can comfortably say that the answer choice is C and that the shaded area falls between 175 and 225 square units, and guess what - the answer is indeed C.
You may have your doubts with this method and believe that calculating the actual area is far more accurate and reliable. You aren’t wrong. Calculating the actual area will remove any room for error that we face in our approximation. However, it takes a much longer period of time.
When I completed the question, I timed myself and it took me 47 seconds to correctly answer the question using the method that I have previously explained. On the other hand, I asked one of my colleagues - Sriram Akula - to answer the question and to specifically calculate the entire shaded area without approximating. Sriram, I must add, is a very good mathematician and comfortably scored a perfect 36 on the ACT Math question without breaking a sweat. However, without approximating, he took 287 seconds to complete the question. That is 240 longer than by using my method. Imagine how many more points you could score with 240 more seconds. Moreover, just within the first two questions in this post we have already saved about 270 seconds, 4 and a half minutes. Considering, the ACT Math Section is very tight for time, every second really does count and this time saving will significantly boost your score.
Question Three
This question tackles your knowledge of trigonometric functions and unit circles. Have a look at the image below.

Okay, so, immediately, we see the words unit circle and we also see an inequality. Many students would begin by visualising their unit circle and trying to figure out where the value would fit in and compare it to the answer choices. However, I am not one for unit circles, simply because it is much more effective and mathematically sound to just consider the actual trigonometric function.
Thus, what is this question really asking us? Well, we just need to find the range of values of θ for which cos(θ) is less than -root(3)/2. If we sketch a basic cosine graph, we can use the sketch and mathematical reasoning to quickly work out the range of values. You could use a graphical calculator for this; however, it is not going to give you exact values for the angles, like the ones shown in the answer choices. By knowing a general sketch for the cosine function, I was able to very quickly sketch the respective function, cos(θ), as shown below.
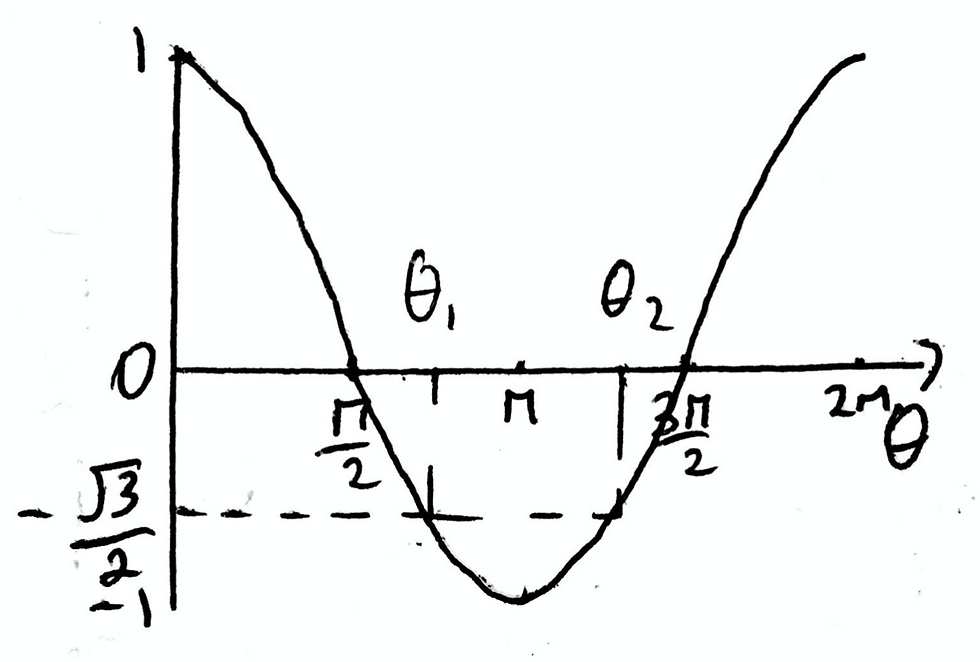
If you were doing this question on the actual ACT exam, there is no need to sketch the function as neatly as I have done; I just wanted it to be neat for you all to see. Now, we can quickly work out what θ1 is by entering arccos(-root(3)/2) into the calculator. This will give us θ1 and only θ1! When we do so, we get 5π/6. This is the lower interval of our range of values. How do we know this? Well, because we sketched the graph and the calculator outputs the smallest positive angle that corresponds to that particular value. Looking at the answer choices, only one of the choices has a lower interval of 5π/6. Thus, since I am confident in my graph sketching abilities, and you should be too, I know that the answer is therefore D. This is a much easier method than utilising a unit circle as there is less to remember. You don’t need to remember the logistics behind the unit circle and how it changes depending on which one of the four quadrants you are in. Rather, you just have to sketch the graph of y = cos(θ) and y = -root(3)/2, like I did before; from here, we just put in one calculation into our trusty calculator and viola - we have a lower interval and thus the answer to the question.
But let’s suppose we had two answer choices with a lower value of 5π/6, how would we discern what is the correct answer? Well, the beauty of trigonometric functions is that they have a numerous amount of axes of symmetry. In this case, we can easily see that y = cos(θ) is symmetrical about x = π. Thus, the difference between θ1 and π is exactly the same as the difference between θ2 and π. Thus, we can simply compute π - θ1 and add this to π in order to work out θ2. When we sub in our value of θ1 as 5π/6, we obtain 7π/6 as our value of θ2. This is the exact upper limit for the answer choice D, which we already established to be the correct answer.
We didn’t have to use the unit circle at all! Remember, whenever a question tells you how to answer it, you don’t have to follow what they say - it is only a recommendation. In this case, we found a much quicker method. Once you are more confident with sketching trigonometric functions and finding the respective values by using the functions’ symmetrical features, you will be able to answer a question like this very quickly. In fact, this question took me 10-15 seconds to complete under timed conditions. Thus, I have an extra 45-50 seconds to spend on a question that is more challenging and perhaps has no shortcuts.
Let’s move onto our fourth question shall we?
Question Four
This next question is a style of question that trips up a lot of students. It involves figuring out certain properties of numbers. Note that you do not need to remember this property but rather you can simply work it out by trial and error. Have a look at an image of the past-ACT question below:

This may look very confusing to some students but let us quickly break it down. We have a number that can essentially be represented as tu. The reverse of this number is therefore ut. This is all information that is given in the question.
Now, many students will begin to panic and skip this question as they cannot figure it out. But, whenever you are stuck on a question like this - and they do come up quite often towards the end of the ACT Math Section - just substitute in some values.
Let’s set x to be 74. Ergo, the reverse of this number, y, will be 47. We can then calculate x - y as this is what is mentioned in the question, which comes out to be 27. From here, we can clearly tell that the answer is not E.
Moreover, as we know t > u, the answer can not be B as this would result in a negative number. So, that is two answer choices eliminated right off the bat. Looking at F, if we substitute in our respective values for t and u, we get 27 as our answer indeed. However, let’s try H and J, just in case. For answer choice H, we would get 59, which is by no means 27. Likewise, answer choice J would yield an answer of 21. Therefore, we can comfortably put F as our final answer.
We didn’t need to do any complex algebra; rather we just simply had to substitute in a random two-digit number and perform the relevant calculations to see which answer choice gives the correct value for x - y. There is no need to check it on a different two-digit number as this rule must work for every two-digit number. If it doesn’t work for one, like 74, it’s not our correct answer.
I hope you have learnt a lot so far. We are almost finished; however, we still have one more exciting and difficult question to go.
Question Five
Let’s have a crack at one last question. This one is a relatively short one, but it uses a very useful mathematical ‘trick’. As always, have a look at an image of the question below.
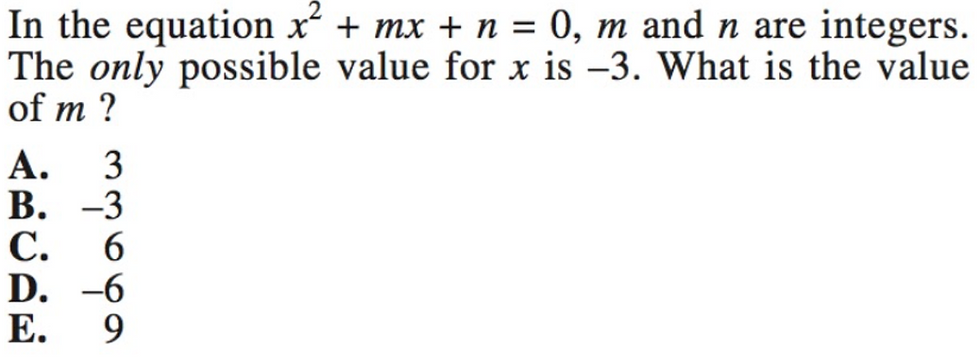
Upon seeing this question, many students will try and substitute in x = -3 into the equation and equate it to 0. However, if we follow such a method, we will simply get stuck with the following equation that cannot be solved without any extra information.
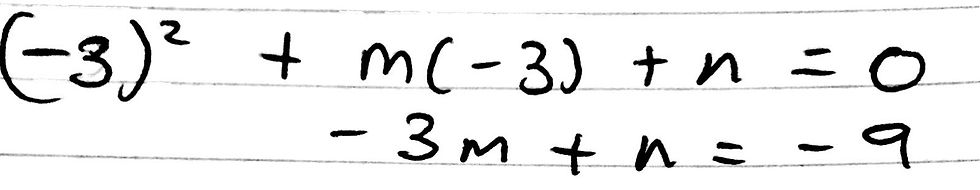
Therefore, the majority of students will simply leave the question here as, without realising one little ‘trick’, the question does not seem to contain enough information. But, as with every question, the question has given us all the information that we need. You see, the key to answering this question lies in the following words: “the only possible value for x is -3”.
Thus, there is what we call a repeated root at x = -3. This also means that the discriminant of the function is equal to 0. The discriminant of a quadratic function can give us a lot of information regarding the nature of the polynomial function.
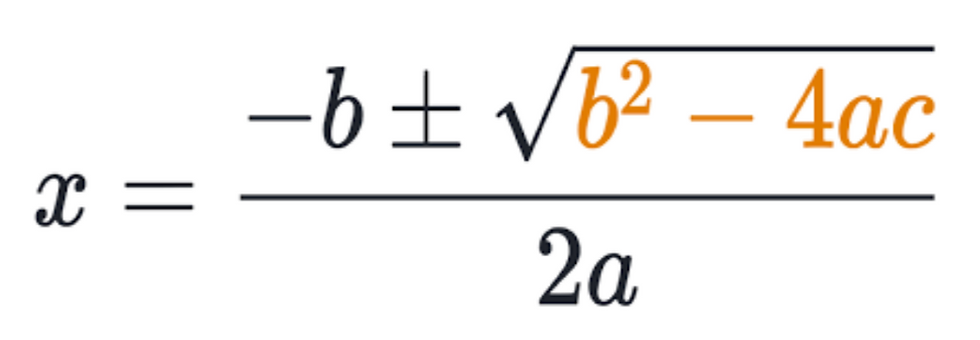
The discriminant is highlighted in orange in the above image. If the discriminant is > 0, the quadratic function has two real roots as shown in the image below. This is due to the fact that a square root can either have a negative or positive value, resulting in two different values for x that result in an output of 0 - otherwise known as two different roots.
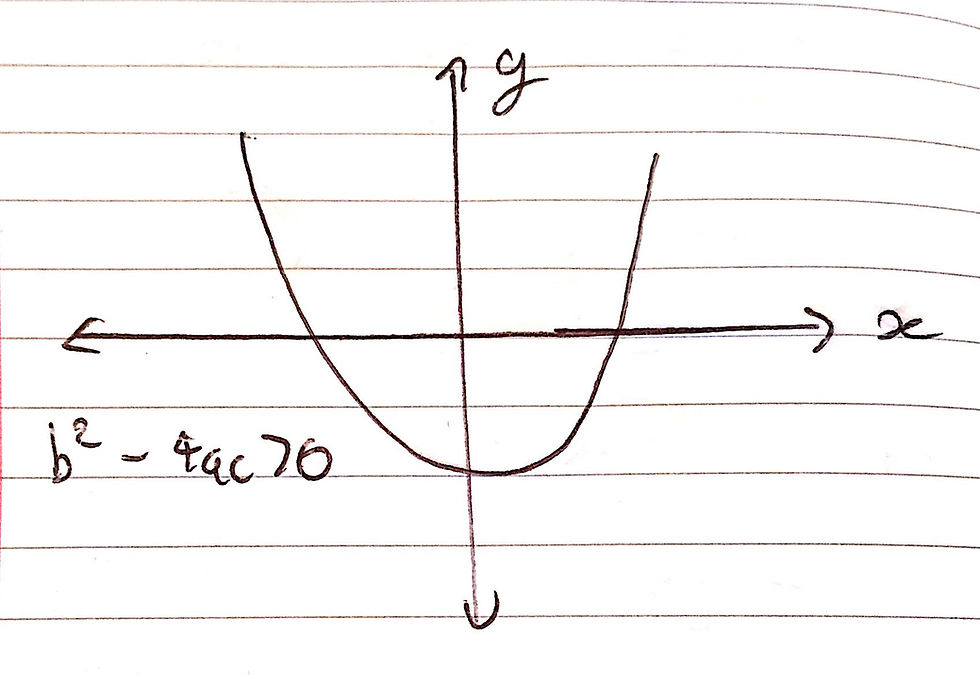
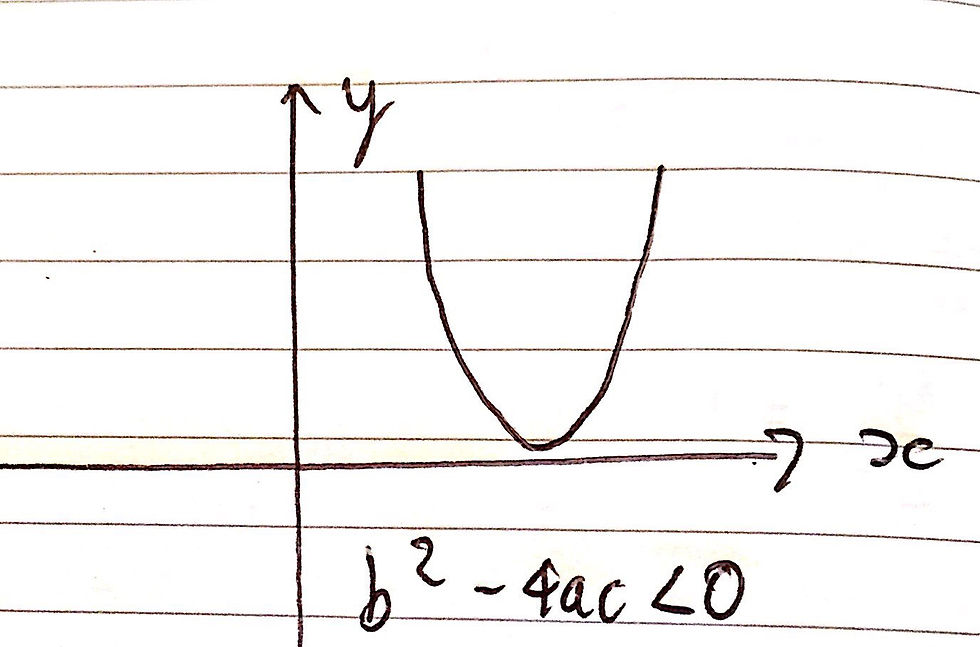
If the discriminant is < 0, the quadratic function has no real roots as can be seen in the sketch below. This is due to the fact that the square root of a negative number is imaginary and therefore the quadratic can have no real roots.
However, if the discriminant = 0, the quadratic has one repeated real root. This is due to the fact that the square root inside the quadratic formula will have an output of 0. Thus, there are no ‘positive’ or ‘negative’ variations of the square root, resulting in the only root being equal to -b/2a. In our case, the quadratic function looks a little bit like this:
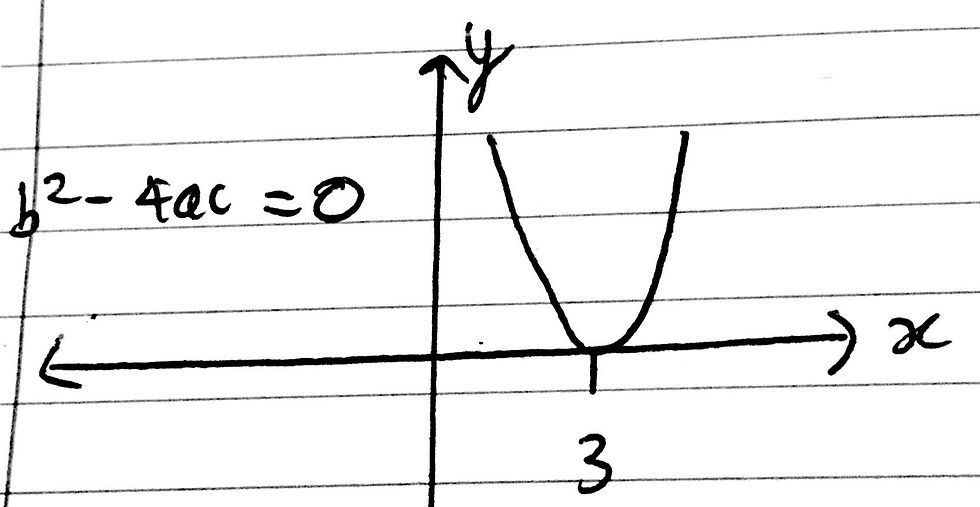
Therefore, we now have our ‘extra bit of information’. We know that the discriminant of our original quadratic function is equal to 0 as we know that the quadratic has a repeated root. Thus, we know that the quadratic equation must be (x-3)^2, resulting one repeated root at x = 3.
We can thus expand (x-3)^2 and find out the value of m and n as I have done so below.
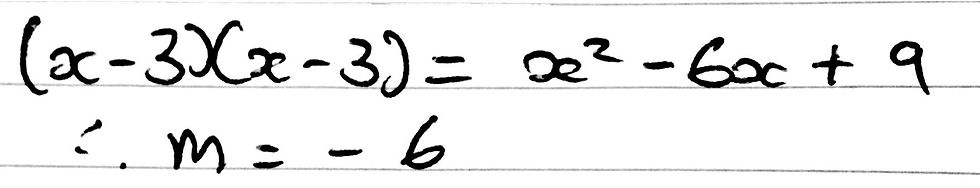
The answer is therefore D. We can also use the discriminant to set up equations and for all sorts, really. It is an invaluable tool.
I hope that you have found this post useful. As you can see, the ACT Math Section does throw in some very tricky questions from time to time; however, they are much easier than they seem. When you see a difficult question, take a deep breath before starting, think about what exactly the question is asking you to solve, and, finally, employ some of the tactics that we have covered in this post. If you have any questions, feel free to leave them down in the comments below. Thank you for reading!



Comments