Introduction
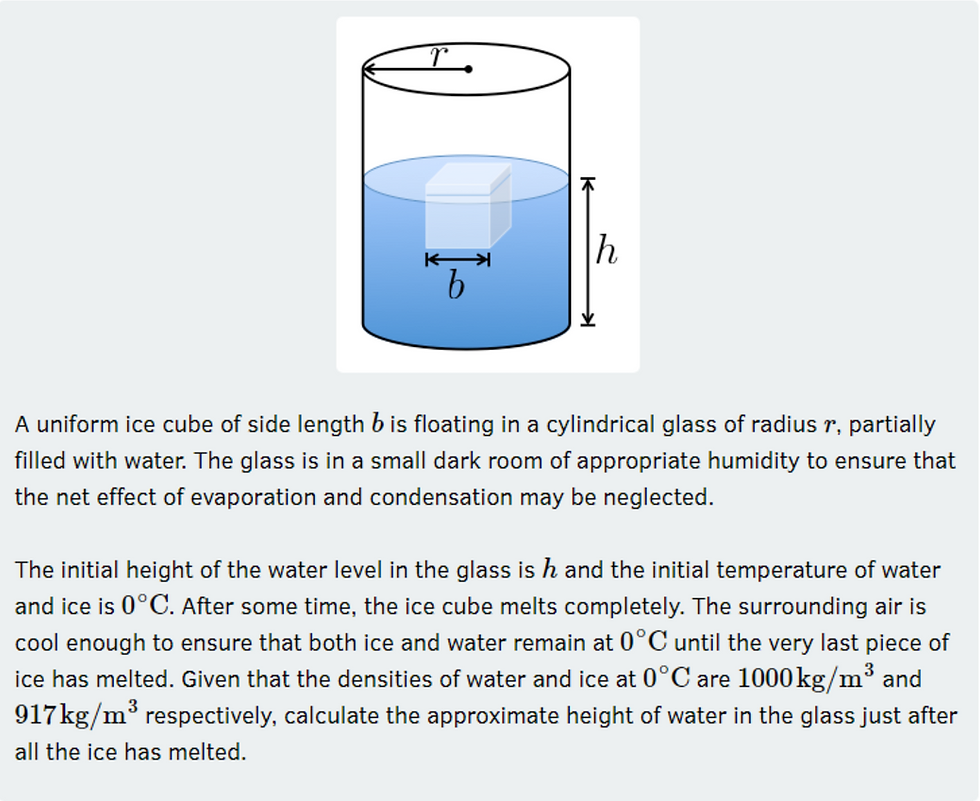
(Photo was sourced: https://i-want-to-study-engineering.org/q/ice_cube/)
This is a very common question that tends to puzzle many people, while also sparking much debate. In fact, I remember one of my friends saying "how is it possible to figure this out without knowing what proportion of the ice is initially in the water?". In my opinion, the key is to put all the information that we know on paper and work from there; this problem can be simplified into two smaller problems as I will do so below.
Part 1: Archimedes’ Principle
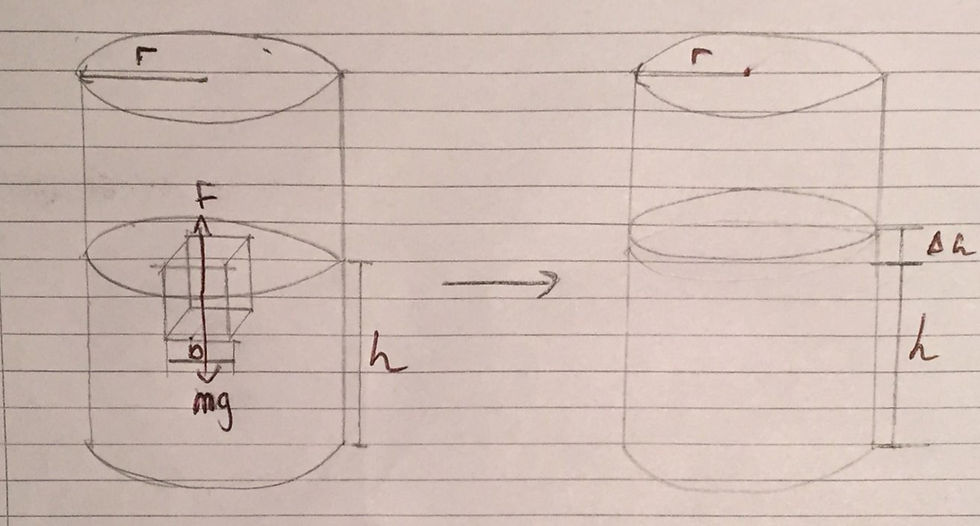
Archimedes’ principle states that the upward buoyant force, labelled as F, which is exerted on a body (in this case, our ice cube), whether fully or partially submerged, is equal to the weight of the fluid that the body displaces. Therefore, if we imagine that the ice cube is suddenly removed (notice, not melted), the height, h, of the water level should fall, as the ice cube is no longer displacing the water.
As the ice cube is in equilibrium, resolving forces vertically should give the result, F=mg, where mg is the weight of the ice cube. This result is useful as ultimately we need to find out what volume of the water, which I will label Vd, is displaced by the ice cube. Subsequently, we can figure out the change in the height level, Δh1, by dividing this displaced volume, Vd, by -πr^2 (as this is the cross-sectional area of the cylinder). The negative indicates that there is a fall in the water level.
Returning to the fact that F=mg, we can express the mass of the ice cube, m, in terms of its density and volume (as we know that m=ρice*Vice, where ρice is the density of the ice cube and Vice represents its volume). This should give the result F=ρice*Vice*g. We can then express the buoyant force, F, in terms of the density and volume of the displaced water (recall that due to Archimedes’ principle, the buoyant force is equal to the weight of the water displaced). We can then rearrange to obtain an expression for the volume of the water displaced, Vd, as I have done so below:
Thus, this allows us to find an overall expression of the change in the height of the water level as I have included below:
Part 2: Conservation of Mass
Remember, however, that we assumed that the ice cube was removed and not melted. We must now remove this assumption and calculate the change in the water level due to the ice cube melting. Essentially, the height of the water level will decrease due to the fact that the ice cube is no longer displacing any water, but will also increase as the mass of the ice cube must be conserved as it melts into water. We must find out whether this increase in the water level is smaller, equal to, or greater than our previously calculated decrease. This part is relatively straightforward as we simply use the equation, ρ=(m/V), to rearrange for the volume of the water, which I will label as Vw, knowing that the mass of the ice cube must be conserved. I have included my workings below:
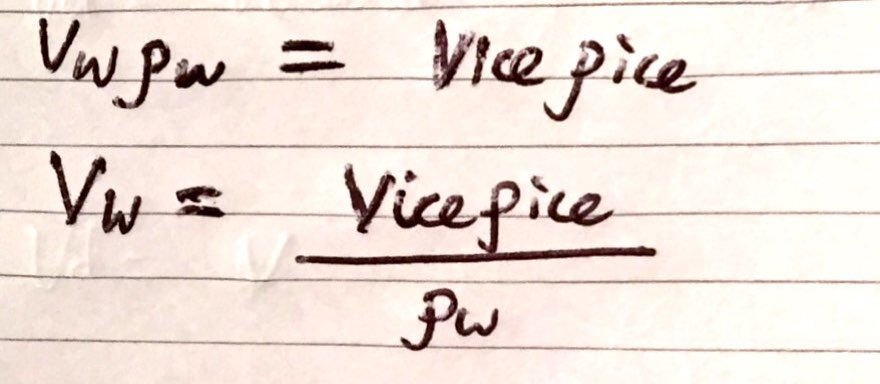
From here, we just use the fact that Vw / πr^2 gives us our change, Δh2, in the height of the water level. Notice that there is no negative this time as the water level will rise. I have included an image of the expression below:
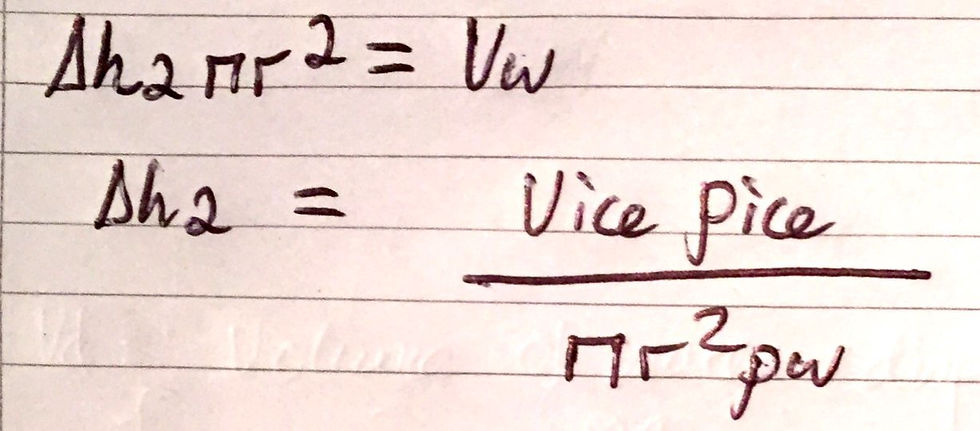
Overall Change:
Thus, the overall change in the height of the water level, Δh, is the sum of Δh1 and Δh2. It should be clear that the final sum is 0. In other words, the water level doesn’t change! I have included an image of this below:
I thought this was a really cool problem when I first heard about it. My gut reaction was to say increase but I then remembered about Archimedes’ principle. However, by using relatively simple mathematics, we have been able to prove that the height of the water level should not change! Hope you have enjoyed reading this post. Feel free to ask any questions that you may have.
Comments