Sorting Algorithms

What is a Sorting Algorithm?

A sorting algorithm is used to arrange an array or list of elements based on a comparison operator. For example, you can order elements based on their ASCII values or you can order numbers based on their size, and for each of these cases a different comparison operator would be used.

What types of sorting algorithms are there?

Here are a few of the main sorting algorithms:

• Selection Sort

• Bubble Sort

• Merge Sort

• Insertion Sort

• Quick Sort

• Heap Sort

• Strand Sort

• Bucket Sort

In this post we will be taking a look at the first three algorithms as these are the main ones you are likely to come across in computer science. But first we must take a look at something called Big O Notation.

What is Big O Notation?

Big O Notation is used to help us compare the efficiency of different approaches to a problem.

Examples of Big O Notation

O(1) also means constant time - this is used to show that no matter the size of the input array, the function will still require only one step. Therefore the input array could be 1 item or 10,000 items, but the function will only require one step.

O(n) also means linear time - this is where n is the number of items in the array and so the more items the array consists of the longer the code will take to run. If n is 10, the code must complete a task 10 times and if n is 1000, the code must complete this task 1000 times which increases the run time to be 100 times as long as before.

O(n^2) also means quadratic time - this is generally when you have nested loops (a for loop within another for loop). If the array has n items, the outer loop will run n times and the inner loop must run n times for each iteration of the outer loop which gives a run time of n^2.

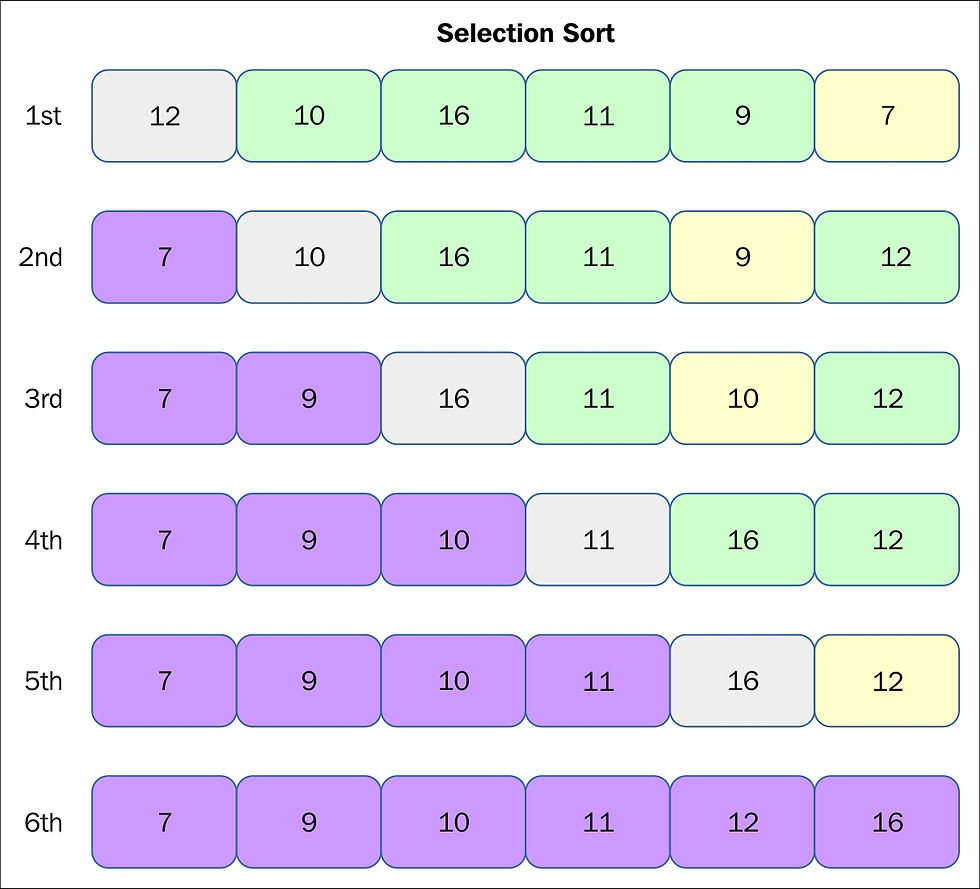
Selection Sort

• The smallest unsorted element in the array is found and swapped with the first unsorted element in the array

• Here is a short diagram which helps to explain the process:

• The run time is O(n^2) due to the use of two nested loops (take a look at the Python program below which shows this sorting algorithm)

• n represents the number of elements within the list

• A benefit of this sorting algorithm is that it will never need to make more than O(n) swaps

Bubble Sort

• This is the simplest algorithm which works by swapping the adjacent pairs of elements if they are out of order

• It effectively bubbles larger elements to the right and smaller ones to the left

• Multiple passes can be completed to sort the algorithm, here is an example of a bubble sort:

• The worst case run time for a bubble sort is O(n^2) which occurs when the array is in reverse order

• The best case scenario is O(n) which occurs when the array is already sorted

Bubble Sort Python Program

How to code a Bubble Sort

When coding this sorting algorithm nested for loops are required to be able to complete multiple passes of the algorithm.

The first for loop is completed n number of times where n is the length of the array. Then the second for loop consists of the main bulk of the code where the swapping takes place, this loop iterates n-i-1 number of times where i is the value of the initial loop.

Merge Sort

• This method requires splitting the array into several sub-arrays and then merging them back together in the correct order

• In all cases, worst, best and average, the merge sort always divides the array into two halves and this takes linear time to merge the two halves

• In Big O Notation the run time is O(nLogn)

• The merge sort can be slightly complicated to understand, therefore, here are some diagrams to help illustrate this sort and help you wrap your head around things:

Merge Sort Process

What are the steps involved in a merge sort?

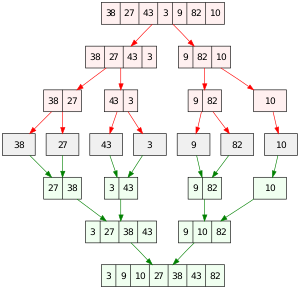
1. Divide the array into two parts

2. Continue dividing until you separate each element into single parts

3. Sort the elements from smallest to largest by comparing two groups at a time and form groups of ordered elements

4. Merge the divided sorted arrays together

5. The array has been sorted